
题目列表(包括答案和解析)
(本题6分) 我们已经知道,利用面积的不同表示方法可以写出一个代数恒等式,例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图1的图形面积的不同表示方法来表示。
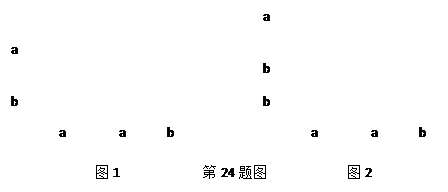
(1)请写出图2所解释的代数恒等式:________________________;
(2)利用上述方法画出一个几何图形说明代数恒等式:(a+3b)(a+b)=a2+4ab+3b2的正确性。
| a2 | a2 | ab |
| ab | ab | b2 |
| ab | ab | b2 |
| a2 | a2 | ab |
| ab | ab | b2 |
解:
(本题6分) 我们已经知道,利用面积的不同表示方法可以写出一个代数恒等式,例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图1的图形面积的不同表示方法来表示。
(1)请写出图2所解释的代数恒等式:________________________;
(2)利用上述方法画出一个几何图形说明代数恒等式:(a+3b)(a+b)=a2+4ab+3b2的正确性。
|
a2 |
a2 |
ab |
|
ab |
ab |
b2 |
|
ab |
ab |
b2 |

|
a2 |
a2 |
ab |
|
ab |
ab |
b2 |
解:
 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题: ,试求sad A的值
,试求sad A的值
|
 | |||
 | |||
(本题满分10分)在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
(1)实验操作: 在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:

(2)观察发现:任一次平移,点P可能到达的点在我们学过的一种函数的图象上,如:平移1次后在函数
的图象上;平移2次后在函数
的图象上……由此我们知道,平移 次后在函数
的图象上.(请填写相应的解析式)
次后在函数
的图象上.(请填写相应的解析式)
(3)探索运用:点P从点O出发经过 次平移后,到达直线
次平移后,到达直线 上的点Q,且平移的路径长不小于50,不超过56,求点Q的坐标.
上的点Q,且平移的路径长不小于50,不超过56,求点Q的坐标.
、(本题10分)我们知道,对于二次函数y=a(x+m)2+k的图像,可由函数y=ax2的图像 进行向左或向右平移一次、再向上或向下移一次平移得到,我们称函数y=ax2为“基本函数”,而称由它平移得到的二次函数y=a(x+m)2+k为“基本函数”y=ax2的“朋友函数”。左右、上下平移的路径称为朋友路径,对应点之间的线段距离 称为朋友距离。
称为朋友距离。
由此,我们所学的函数:二次函数y=ax2,函数y=kx和反比例函数 都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”。
如一次函数y=2x-5是基本函数y=2x的朋友函数,由y=2x-5=2(x-1)-3朋友路径可以是向右平移1个单位,再向下平移3个单位,朋友距离= .
.
1.(1)探究一:小明同学经过思考后,为函数y=2x-5又找到了一条朋友路径为由基本函数y=2x先向 ,再向下平移7单位,相应的朋友距离为 。
2.(2)探究二:已知函数y=x2-6x+5,求它的基本函数,朋友路径,和相应的朋友距离。
3.(3)探究三:为函数 和它的基本函数
和它的基本函数 ,找到朋友路径,
,找到朋友路径,
并求相应的朋友距离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com