
题目列表(包括答案和解析)
(10分,当总分已达95分时,此题得分不计入总分;当总分不到95分时,计入总分.但计入总分后,总分不得超过95分.)
 如图为3×3的正方形,求∠1+∠2+∠3+…+∠7+∠8+∠9的和.
如图为3×3的正方形,求∠1+∠2+∠3+…+∠7+∠8+∠9的和.
阅读材料:
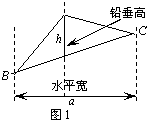
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:![]() ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
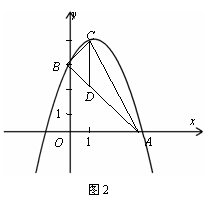
如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及![]() ;
;
(3)是否存在一点P,使S△PAB=![]() S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
(1)![]() 还成立吗?请说明理由
还成立吗?请说明理由
(2)试找出S△ABD,S△BED,S△BDC间的关系式,并说明理由。

(本题满分12分)在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.
观察计算:
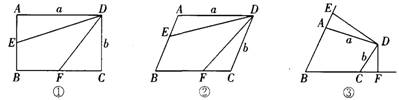
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF 的面积S四边形DEBF=_______.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=_______.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=_______.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=_______,请说明理由.
解决问题:
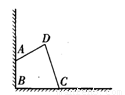
如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.
如图,直线![]() 与x轴交于点A,与y轴交于点B,以线段AB为直径作⊙C,抛物线
与x轴交于点A,与y轴交于点B,以线段AB为直径作⊙C,抛物线![]() 过A、C、O三点.
过A、C、O三点.
(1) 求点C的坐标和抛物线的解析式;
(2) 过点B作直线与x轴交于点D,且OB2=OA·OD,求证:DB是⊙C的切线;
(3) 抛物线上是否存在一点P, 使以P、O、C、A为顶点的四边形为直角梯形,如果存在,求出点P的坐标;如果不存在,请说明理由.
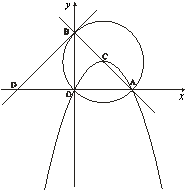
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com