阅读并解答
看下面的问题：
从甲地到乙地，可以乘火车，也可以乘汽车．一天中，火车有3班，汽车有2班．那么一天中，乘坐这些交通工具从甲地到乙地共有多少种不同的走法？
因为一天中乘火车有3种走法，乘汽车有2种走法，每一种走法都可以从甲地到乙地，所以共有3+2=5种不同的走法．
一般地，有如下原理：
分类计数原理：完成一件事，在第1类办法中有m₁种不同的方法，在第2类办法中有m₂种不同的方法…在第n类办法中有m_n种不同的方法．那么完成这件事共有N=m₁+m₂+…+m_n种不同的方法．
再看下面的问题：
从甲地到乙地，要从甲地先乘火车到丙地，再于次日从丙地乘汽车到乙地．一天中，火车有3班，汽车有2班，那么两天中，从甲地到乙地共有多少种不同的走法？
这个问题与前一问题不同．在前一问题中，采用乘火车或乘汽车中的任何一种方式，都可以从甲地到乙地．而在这个问题中，必须经过先乘火车、后乘汽车两个步骤，才能从甲地到达乙地．
这里，因为乘火车有3种走法，乘汽车有2种走法，所以乘一次火车再接乘一次汽车从甲地到乙地，共有  3×2=6种不同的走法．
一般地，有如下原理：
分步计数原理：完成一件事，需要分成n个步骤，做第1步有m₁种不同的方法，做第2步有m₂种不同的方法…做第n步有m_n种不同的方法．那么完成这件事共有
N=m₁×m₂×…×m_n种不同的方法．
例：书架的第1层放有4本不同的计算机书，第2层放有3本不同的文艺书，第3层放有2本不同的体育书．
（1）从书架上任取1本书，有多少种不同的取法？
（2）从书架的第1、2、3层各取1本书，有多少种不同的取法？
解：（1）从书架上任取1本书，有3类办法：第1类办法是从第1层取1本计算机书，有4种方法；第2类办法是从第2层取1本文艺书，有3种方法；第3类办法是从第3层取1本体育书，有2种方法．根据分类计数原理，不同取法的种数是
N=m₁+m₂+m₃=4+3+2=9
答：从书架上任取1本书，有9种不同的取法．
（2）从书架的第1、2、3层各取1本书，可以分成3个步骤完成：第1步从第1层取1本计算机书，有4种方法；第2步从第2层取1本文艺书，有3种方法；第3步从第3层取1本体育书，有2种取法．根据分步计数原理，从书架的第1、2、3层各取1本书，不同取法的种数是N=m₁×m₂×m₃=4×3×2=24
答：从书架的第1、2、3层各取1本书，有24种不同的取法．
完成下列填空：
（1）从5位同学中产生1名组长，1名副组长有______种不同的选法．
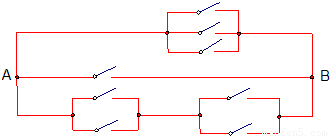
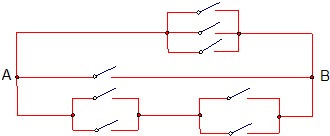
（2）如图，一条电路在从A处到B处接通时，可以有______条不同的路线．
（3）用数字0、1、2、3、4、5组成______个没有重复数字的六位奇数．
（4）一种汽车牌照由2个英文字母后接4个数字组成，且2个英文字母不能相同，则不同牌照号码的个数是______．