
题目列表(包括答案和解析)
(1)如果用整个圆表示总体,那么扇形A、B、C、D各占总体的几分之几?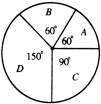
(2)若整个圆代表你们学校的人数,且知道扇形A代表70人,试计算出扇形B、C、D各代表多少?
(3)若用整个圆代表一个乡的耕地面积,且知道A块地有4500公顷,那么D块地有多少公顷?
 观察下列图形,阅读下面的相关文字并回答以下问题:
观察下列图形,阅读下面的相关文字并回答以下问题: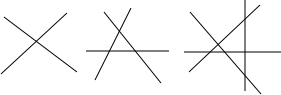 观察下列图形,阅读下面的相关文字并回答以下问题:
观察下列图形,阅读下面的相关文字并回答以下问题:
| 5 |
| 5 |
| 3 |
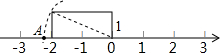

 的B点(保留作图痕迹).
的B点(保留作图痕迹).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com