填空并完成推理过程．

　　　（1）如图（1），，（已知）

　　　　　　　　　　＝．(　　　　　　　　　　　　　　　)

　　　　　　，(已知)

　　　　　　＝　　　　　　，(　　　　　　　　　　　　　　)

　　　　　　＝　　　　　　；(　　　　　　　　　　　　　　　)

　　　（2）如图（2），已知，，．试判断与的关系，并说明你的理由．

　 解：，理由是：，．(已知)

　　　　　　　　　　　　＝　　　　　＝．(　　　　　　　　)

　　　　　　　，(　　　　　　　　)

　　　　　　　，即．

　　　　　　　　　　　　　　　　　　；(　　　　　　　　　　　　　　　　

(3) 如图(3)，点为上的点，点为上的点，，，试说明：．

　　解：，(已知)，(　　　　　　　　　　　　　)

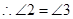　　　　　　，(等量代换)

　　　　　　　　　　　　，(　　　　　　　　　　　　　　　　　　　　)

　　　　，(　　　　　　　　　　　　　　　　　　　　　)

　　　　又，(已知)

　　　　，(　　　　　　　　　　　　　)

　　　　．(　　　　　　　　　　　　　　　　　　　　　　　　　　　)

（1）    本次活动共有多少件作品参评？

（2）    哪组上交的作品数量最多？有多少件？

（3）    经过评比，第四组与第六组分别有10件与2件获奖，那么这两组中哪组的获奖率较高？

　　　　　　　　　　　　　　　　　　　　    频率

　　　　　　　　　　　　　　　　　　   6

　　　　　　　　　　　　　　　　  　　 5

　　　　　　　　　　　　　　　　　　   4

　　　　　　　　　　　　　　　　　　   3

　　　　　　　　　　　　　　　　　　   2

　　　　　　　　　　　　　　　　　　   1  　　　　　　　　　　   日期

    　　　　　　　　　　　　　　　　　　　　1  6 11 16 21 26  31

如下图，E是ABCD的边AB上的一点，射线CE交BD于F，交DA的延长线于点G，AE：EB=1：2．图中有哪些位似三角形?位似中心分别是哪一个点?位似比分别为多少?填在下表中．

探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法。请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC,BD为腰AC上的高。

(1)若BD=h，M时直线BC上的任意一点，M到AB、AC的距离分别为。

①　　 若M在线段BC上，请你结合图形①证明：= h；　　　　　　　　　　

②　　 当点M在BC的延长线上时，，h之间的关系为　　　　　 （请直接写出结论，不必证明）　　　　　　　　　　　　　　　　　　　　　　　　　

（2）如图②，在平面直角坐标系中有两条直线：y = x + 6 ； ：y = -3x+6 若上的一点M到的距离是3，请你利用以上结论求解点M的坐标。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图②