
题目列表(包括答案和解析)


 与x轴有两个不同的交点。
与x轴有两个不同的交点。
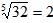 ,因为(±2)4=16,所以2和-2都是16的四次方根,记作
,因为(±2)4=16,所以2和-2都是16的四次方根,记作 ;
; 且
且 ,求abxy的六次方根。
,求abxy的六次方根。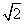 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用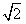 -1来表示
-1来表示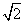 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为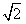 的整数部分是1,将这个数减去其整数部分,差就是小数部分。
的整数部分是1,将这个数减去其整数部分,差就是小数部分。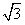 =x+y,其中x是整数,且0<y<1,求x-y的相反数。
=x+y,其中x是整数,且0<y<1,求x-y的相反数。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com