
题目列表(包括答案和解析)
 (2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
(2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.| AB |
| BC |
| CE |
| CG |
 纸片沿对角线
纸片沿对角线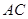 剪开,得
剪开,得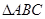 和
和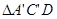 ,如图(1-1)所示.将
,如图(1-1)所示.将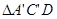 的顶点
的顶点 与点
与点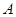 重合,并绕点
重合,并绕点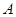 按逆时针方向旋转,使点
按逆时针方向旋转,使点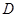 、
、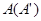 、
、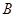 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.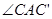 =_______;
=_______;
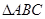 中,
中,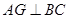 于点
于点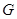 ,以
,以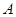 为直角顶点,分别以
为直角顶点,分别以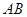 、
、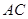 为直角边,向
为直角边,向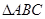 外作等腰
外作等腰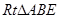 和等腰
和等腰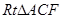 ,过点
,过点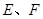 作射线
作射线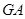 的垂线,垂足分别为
的垂线,垂足分别为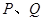 . 求证:
. 求证: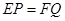 .
.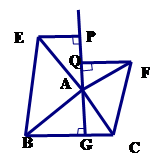
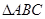 中,
中,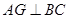 于点
于点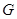 ,以
,以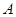 为直角顶点,分别以
为直角顶点,分别以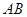 、
、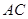 为直角边,向
为直角边,向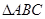 外作
外作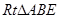 和
和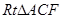 ,过点
,过点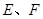 作射线
作射线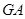 的垂线,垂足分别为
的垂线,垂足分别为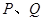 .若
.若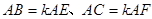 ,试探究
,试探究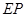 与
与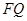 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.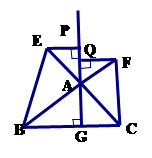
题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题探究:
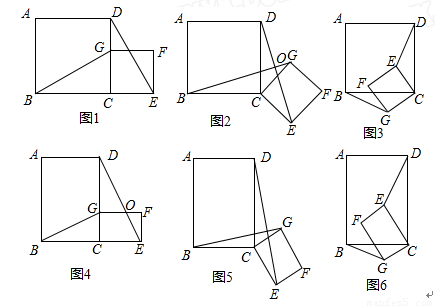
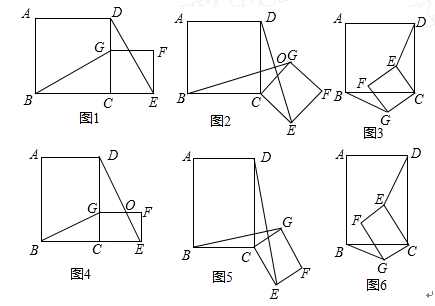
1.(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:
2.(2)若将原题中的“正方形”改为“矩形”(如图所示),且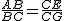 =k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
=k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
拓展应用:
3.(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
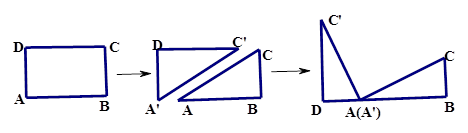
将矩形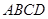 纸片沿对角线
纸片沿对角线 剪开,得
剪开,得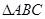 和
和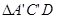 ,如图(1-1)所示.将
,如图(1-1)所示.将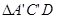 的顶点
的顶点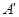 与点
与点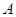 重合,并绕点
重合,并绕点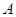 按逆时针方向旋转,使点
按逆时针方向旋转,使点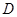 、
、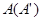 、
、 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.
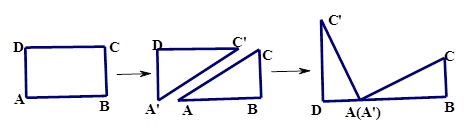
【小题1】观察图可知:与BC相等的线段是______,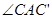 =_______;
=_______;
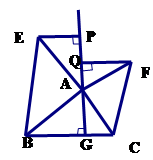
【小题2】如图(2),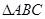 中,
中,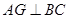 于点
于点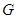 ,以
,以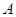 为直角顶点,分别以
为直角顶点,分别以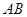 、
、 为直角边,向
为直角边,向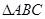 外作等腰
外作等腰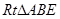 和等腰
和等腰 ,过点
,过点 作射线
作射线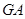 的垂线,垂足分别为
的垂线,垂足分别为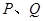 . 求证:
. 求证: .
.
【小题3】如图(3),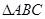 中,
中,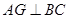 于点
于点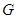 ,以
,以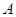 为直角顶点,分别以
为直角顶点,分别以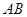 、
、 为直角边,向
为直角边,向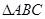 外作
外作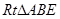 和
和 ,过点
,过点 作射线
作射线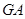 的垂线,垂足分别为
的垂线,垂足分别为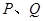 .若
.若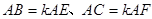 ,试探究
,试探究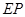 与
与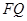 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.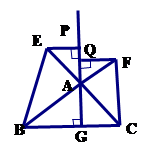
题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题探究:
1.(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:
2.(2)若将原题中的“正方形”改为“矩形”(如图所示),且![]() =k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
=k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
拓展应用:
3.(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com