我们知道：将一条线段AB分割成大小两条线段AC、CB，若小线段CB与大线段AC的长度之比等于大线段AC与线段AB的长度之比，即这种分割称为黄金分割，点C叫做线段AB的黄金分割点．

(1)类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．如图，在△ABC中，∠A＝36°，AB＝AC，∠ACB的角平分线CD交腰AB于点D，请你说明D为腰AB的黄金分割点的理由．

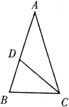
(2)若腰和上底相等，对角线和下底相等的等腰梯形叫作黄金梯形，其对角线的交点为对角线的黄金分割点．如图，AD∥BC，AB＝AD＝DC，AC＝BD＝BC，试说明O为AC的黄金分割点．

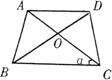
(3)如图，在Rt△ABC中，∠ACB＝90°，CD为斜边AB上的高，∠A、∠B、∠ACB的对边分别为a、b、c．若D是AB的黄金分割点，那么a、b、c之间的数量关系是什么？并证明你的结论．

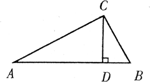
数学课上，同学们探究下面命题的正确性：顶角为36°的等腰三角形具有一种特性，即经过它的某一顶点的一条直线可把它分成两个小等腰三角形．为此，请你解答问题(1)．

(1)如图1，在△ABC中，AB＝AC，∠A＝36°，直线BD平分∠ABC交AC于点D．

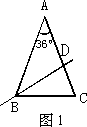
求证：△ABD与△BDC都是等腰三角形．

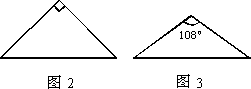
(2)在证明了该命题后，小颖发现：下列两个等腰三角形如图2、图3也具有这种特性．请你在图2、图3中分别画出一条直线，把它们分成两个小等腰三角形，并在图中标出所画等腰三角形两个底角的度数．