
题目列表(包括答案和解析)
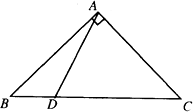
如图,已知在△ABC中,AB=AC,∠BAC=90°,点D是BC上的任意一点,探究:BD2+CD2与AD2的关系,并证明你的结论.
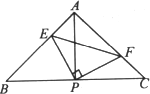
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF,②∠APE=∠CPF,③△EPF是等腰直角三角形,④EF=AP,⑤S四边形AEPF=![]() S△ABC.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的序号有________.
S△ABC.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的序号有________.
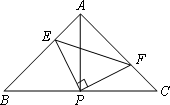
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:
①AE=CF,②∠APE=∠CPF,③△EPF是等腰直角三角形,④EF=AP,⑤![]() .当∠EPE在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的序号有________.
.当∠EPE在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的序号有________.
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE________度;
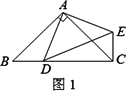
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
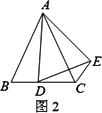
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
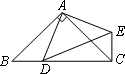
(2)设∠BAC=α,∠BCE=β.
①如图,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
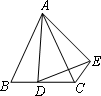
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com