
题目列表(包括答案和解析)
 已知如图,直线y=-
已知如图,直线y=-| 3 |
| 3 |
| ||
| 3 |
 已知如图,直线y=-
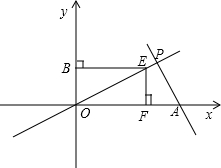
已知如图,直线y=- x+4
x+4 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y= x相交于点P.
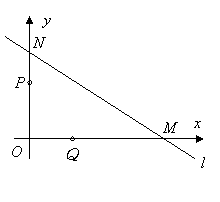
x相交于点P.如图, 直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() .点
.点![]() 从点
从点![]() 出发,
出发,
以每秒1个单位长度的速度沿![]() →
→![]() 方向运动,点
方向运动,点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() →
→![]() 的方向运动.已知点
的方向运动.已知点![]() 同时出发,当点
同时出发,当点![]() 到达点
到达点![]() 时,
时,![]() 两点同时停止运动, 设运动时间为秒.设四边形MNPQ的面积为
两点同时停止运动, 设运动时间为秒.设四边形MNPQ的面积为![]() .
.
(1)求![]() 关于的函数关系式,并写出自变量的取值范围;
关于的函数关系式,并写出自变量的取值范围;
(2)问t几秒时四边形面积![]() 有最值,请求出相应的面积。
有最值,请求出相应的面积。
如图,直线![]() 与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0).
与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0).

(1)求该二次函数的关系式;
(2)设该二次函数的图象的顶点为M,求四边形AOCM的面积;
(3)有两动点D、E同时从点O出发,其中点D以每秒![]() 个单位长度的速度沿折线OAC按O→A→C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O→C→A的路线运动,当D、E两点相遇时,它们都停止运动.设D、E同时从点O出发t秒时,△ODE的面积为S.
个单位长度的速度沿折线OAC按O→A→C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O→C→A的路线运动,当D、E两点相遇时,它们都停止运动.设D、E同时从点O出发t秒时,△ODE的面积为S.
①请问D、E两点在运动过程中,是否存在DE∥OC,若存在,请求出此时t的值;若不存在,请说明理由;
②请求出S关于t的函数关系式,并写出自变量t的取值范围;
③设S0是②中函数S的最大值,那么S0=________.
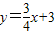 与x轴、y 轴分别交于A、B两点,已知点C(0,-1)、D(0,k),且0<k<3,以点D为圆心、DC为半径作⊙D,当⊙D与直线AB相切时,k的值为( )
与x轴、y 轴分别交于A、B两点,已知点C(0,-1)、D(0,k),且0<k<3,以点D为圆心、DC为半径作⊙D,当⊙D与直线AB相切时,k的值为( )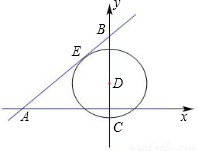




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com