
题目列表(包括答案和解析)
(本题12分) 如图,已知二次函数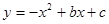 的图象与
的图象与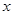 轴交于点
轴交于点 、
、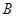 ,与
,与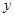 轴交于点
轴交于点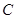 ,其顶点为
,其顶点为 ,且直线
,且直线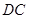 的解析式为
的解析式为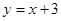 .
.
【小题1】(1) 求二次函数的解析式.
【小题2】(2) 求△ABC外接圆的半径及外心的坐标;
【小题3】(3) 若点P是第一象限内抛物线上一动点,求四边形ACPB的面积最大值.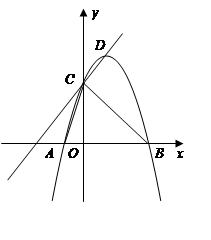
(本题12分)魔术师为大家表演魔术. 他请观众想一个数,然后将这个数按以下步骤操作:
魔术师立刻说出观众想的那个数.
(1)如果小明想的数是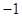 ,那么他告诉魔术师的结果应该是 ;
,那么他告诉魔术师的结果应该是 ;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,我们发现假设想的数为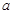 时,请按魔术师要求的运算过程写成代数式?
时,请按魔术师要求的运算过程写成代数式?
(4)化简(3)所列的代数式并化简,请你用一句话说出其中的奥妙.
(本题12分) 如图,在平面直角坐标系中,二次函数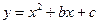 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.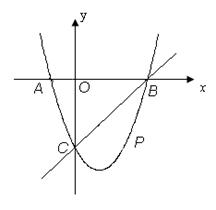
(1)求b,c的值.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形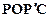 ,那么是否存在点P,使四边形
,那么是否存在点P,使四边形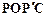 为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
(本题12分)已知二次函数的图象如图所示.
【小题1】(1)求二次函数的解析式及抛物线顶点M的坐标;
【小题2】(2)若点N为线段BM上的一点,过点N作x轴的垂线,垂足为点Q.当点N在线段BM上运动时(点N不与点B,点M重合),设NQ的长为t,四边形NQAC的面积为s,求s与t之间的函数关系式及自变量t的取值范围;
【小题3】(3)在对称轴右侧的抛物线上是否存在点P,使△PAC为直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由;
【小题4】(4)将△OAC补成矩形,使上△OAC的两个顶点成为矩形一边的两个顶点,第三个顶点落在矩形这一边的对边上,试直接写出矩形的未知的顶点坐标(不需要计算过程).
(本题12分)有一群猴子,一天结伴去偷桃子.分桃子时,如果每只猴子分3个,那么还剩下59个,如果每只猴子分5个,有一只猴子分得的桃子不足5个.你能求出有几只猴子,几个桃子吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com