
题目列表(包括答案和解析)
 ”,这种利用图形直观说明问题的方式体现的数学思想方法叫
”,这种利用图形直观说明问题的方式体现的数学思想方法叫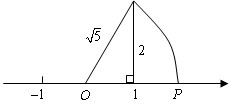
[ ]
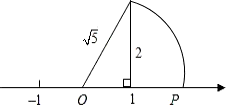 “数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是
“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是 ”,这种利用图形直观说明问题的方式体现的数学思想方法叫
”,这种利用图形直观说明问题的方式体现的数学思想方法叫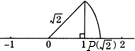 如图所示,“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是
如图所示,“数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是 ”,这种说明问题的方式体现的数学思想方法叫做
”,这种说明问题的方式体现的数学思想方法叫做
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
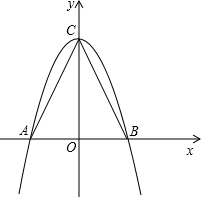 (2012•柳州)如图,在△ABC中,AB=2,AC=BC=
(2012•柳州)如图,在△ABC中,AB=2,AC=BC=| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| x2-2 |
| x2-2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com