
题目列表(包括答案和解析)
如图所示,在矩形ABCD中,∠DBC=29°,将矩形沿直线BD折叠,顶点C落在点E处,则∠ABE的度数是( )
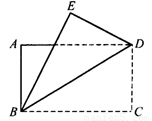
A.29° B.32° C.22° D.61°
| 级数 | 水量基数 (立方米) |
调整后价格 (元/立方米) |
| 第一级 | 0~15(含15) | 2.61 |
| 第二级 | 15~25(含25) | 3.92 |
| 第三级 | 25以上 | n |

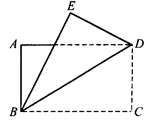
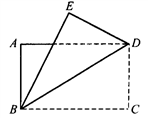
 29、小明坐在学校的凉亭(A)中,绘制了学校的一张简图(如图所示),体育馆在凉亭的正北方向.测得:∠DAE=109°35′,∠EAF=61°35′,且AE平分∠FAC,AB⊥AC.
29、小明坐在学校的凉亭(A)中,绘制了学校的一张简图(如图所示),体育馆在凉亭的正北方向.测得:∠DAE=109°35′,∠EAF=61°35′,且AE平分∠FAC,AB⊥AC.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com