
题目列表(包括答案和解析)
如图,已知正三角形ABC的边长AB是480毫米.一质点D从点B出发,沿BA方向,以每秒钟10毫米的速度向点A运动.
⑴ 建立合适的直角坐标系,用运动时间t(秒)表示点D的坐标;
⑵ 过点D在三角形ABC的内部作一个矩形DEFG,其中EF在BC边上,G在AC边上.在图中找出点D,使矩形DEFG是正方形(要求所表达的方式能体现出找点D的过程);
⑶ 过点D、B、C作平行四边形,当t为何值时,由点C、B、D、F组成的平行四边形的面积等于三角形ADC的面积,并求此时点F的坐标.
 |
如图,已知正三角形ABC的边长AB是480毫米.一质点D从点B出发,沿BA方向,以每秒钟10毫米的速度向点A运动.
⑴ 建立合适的直角坐标系,用运动时间t(秒)表示点D的坐标;
⑵ 过点D在三角形ABC的内部作一个矩形DEFG,其中EF在BC边上,G在AC边上.在图中找出点D,使矩形DEFG是正方形(要求所表达的方式能体现出找点D的过程);
⑶ 过点D、B、C作平行四边形,当t为何值时,由点C、B、D、F组成的平行四边形的面积等于三角形ADC的面积,并求此时点F的坐标.
 |
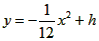 的解析式,并判断它与直线AD的公共点的个数。
的解析式,并判断它与直线AD的公共点的个数。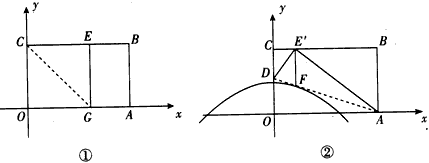
 x2+h过点F,求此抛物线的关系式,并判断它与直线AD的交点的个数;
x2+h过点F,求此抛物线的关系式,并判断它与直线AD的交点的个数;
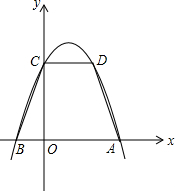 如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC=
如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC=| 10 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com