
题目列表(包括答案和解析)
| 步骤 | 举例说明 | ||||||||||||||||||||||||||||
| 1.自右向左编号 | 某商品条形码为:690123456789X(X为校验码)
| ||||||||||||||||||||||||||||
| 2.从序号2开始,求出偶数位上的数字之和① | 9+7+5+3+1+9=34 | ||||||||||||||||||||||||||||
| 3.①×3=② | 34×3=102 | ||||||||||||||||||||||||||||
| 4.从序号3开始,求出奇数位上的数字之和③ | 8+6+4+2+0+6=26 | ||||||||||||||||||||||||||||
| 5.②+③=④ | 102+26=128 | ||||||||||||||||||||||||||||
| 6.用大于或等于结果④且为10的最小整数倍的数减去④,其差即为校验码值 | 130-128=2 校验码X=2 |
| S |
| 6 |
| m |
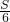 =m;第二步:
=m;第二步: =k;第三步:分别用3、4、5乘k,得三边长”.
=k;第三步:分别用3、4、5乘k,得三边长”.| 步骤 | 举例说明 | ||||||||||||||||||||||||||||
| 1.自右向左编号 | 某商品条形码为:690123456789X(X为校验码)
| ||||||||||||||||||||||||||||
| 2.从序号2开始,求出偶数位上的数字之和① | 9+7+5+3+1+9=34 | ||||||||||||||||||||||||||||
| 3.①×3=② | 34×3=102 | ||||||||||||||||||||||||||||
| 4.从序号3开始,求出奇数位上的数字之和③ | 8+6+4+2+0+6=26 | ||||||||||||||||||||||||||||
| 5.②+③=④ | 102+26=128 | ||||||||||||||||||||||||||||
| 6.用大于或等于结果④且为10的最小整数倍的数减去④,其差即为校验码值 | 130-128=2 校验码X=2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com