
题目列表(包括答案和解析)
如图所示,在长方形ABCD中,横向阴影部分为长方形,另一阴影部分为平行四边形.依照图中标注的数据和小学学过的有关图形的面积公式,计算图中空白部分的面积.

| ||
| 4 |
| π |
| 8 |
 a2-
a2-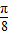 a2.
a2.

 a2-
a2- a2.
a2.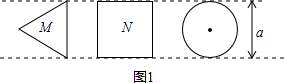
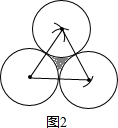
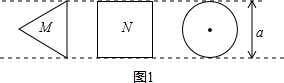
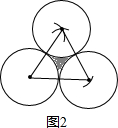
如图1,M,N分别表示边长为a的等边三角形和正方形,P表示直径为a的圆.图2是选择基本图形M,P用尺规画出的图案,![]() .
.
(1)请你从图1中任意选择两种基本图形,按给定图形的大小设计一个新图案,还要选择恰当的图形部分涂上阴影,并计算阴影的面积;(尺规作图,不写作法,保留痕迹,作直角时可以使用三角板)
(2)请你写一句在完成本题的过程中感受较深且与数学有关的话.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com