
题目列表(包括答案和解析)
小明的父母出去散步,从家出发走了20分钟到一个离家300米的报亭母亲随即按原路返回,父亲翻阅了10分钟报纸后,用了15分钟返回家.下面的图象中,正确表示父亲离家时间与距离之间的关系和母亲离家时间与距离之间的关系的是

[ ]
| mh | m-n |
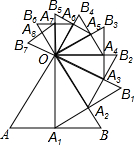 已知等边三角形AOB的边长为32,以AB边上的高OA1为边按顺时针方向做等边三角形OA2B2,与OB相交于A2,如图,按此做法进行下去.
已知等边三角形AOB的边长为32,以AB边上的高OA1为边按顺时针方向做等边三角形OA2B2,与OB相交于A2,如图,按此做法进行下去.| 2 |
| 2 |
| 5 |
| 2 |
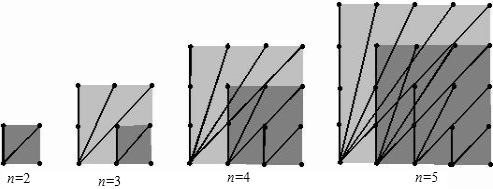
| 钉子数(n) | S值 |
| 2×2 | 2 |
| 3×3 | 2+3 |
| 4×4 | 2+3+( ) |
| 5×5 | ( ) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com