
题目列表(包括答案和解析)
| 第一次 | 第二次 | |
| 甲种货车的数量(单位:辆) | 2 | 5 |
| 乙种货车的数量(单位:辆) | 3 | 6 |
| 累积运货的数量(单位:吨) | y2 | 38 |
| b |
| a |
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| x2-2x+1 |
| x2-1 |
| x-1 |
| x2+x |
| 1 |
| x+2 |
| 4x |
| (x+2)(x-2) |
| 2 |
| 2-x |
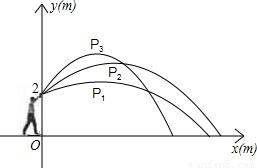
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
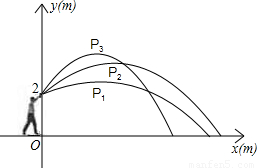
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com