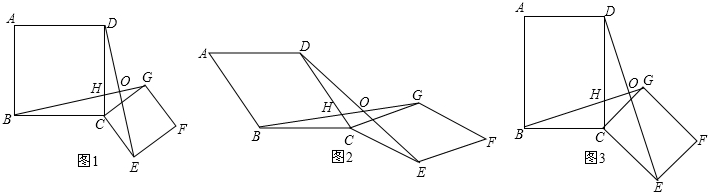
27、如图1,两个不全等的四边形ABCD、四边形CGFE是正方形,连接BG,DE.交DC于H,交CG于K
(1)观察图形,①猜想BG与DE之间长度关系;②猜想BG与DE所在直线的位置关系,并证明你的猜想.
直接回答:连接四边形DBEG四边中点所得四边形是
正方
形
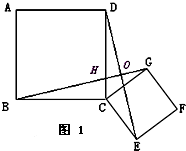
(2)如图2,将原题中正方形改为菱形,且∠BCD=∠GCE=90°.则(1)中的①、②的结论是否成立?若成立,请证明;若不成立,请说明理由.
直接回答:连接四边形DBEG四边中点所得四边形是
正方
形
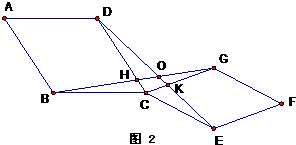
(3)如图3,将原题中正方形改为矩形,且BC=mCG、CD=mCE则(1)中的①、②结论是否成立?不要证明
直接回答:连接四边形DBEG四边中点所得四边形是
矩
形.