练习册

  • 练习册
  • 试题
    D.E.F为△ABC的三边中点.L.M.N分别是△DEF三边的中点.若△ABC的周长为20.则△LMN的周长是 A.15 B.12 C.10 D.5 【查看更多】

     

    题目列表(包括答案和解析)

    D、E、F为△ABC的三边中点，L、M、N分别是△DEF三边的中点，若△ABC的周长为20，则△LMN的周长是（      ）

    A.15      B.12    C.10   D.5

    查看答案和解析>>

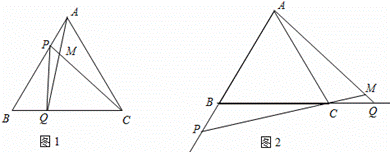
    点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点，点P从顶点A,点Q从顶点B同时出发，且它们的速度都是1cm/s.

    （1）连接AQ、CP交于点M，则在P、Q运动的过程中，∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数；

    （2）当t=            时，△PBQ是直角三角形？

    （3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数．

    查看答案和解析>>

    已知△ABC的三边长为5cm，12cm，13cm，D、E、F分别是三边的中点，则△DEF的面积为


    1. A.
      30cm2
    2. B.
      15cm2
    3. C.
      7.5cm2
    4. D.
      3.75cm2

    查看答案和解析>>

    点D、E、F分别是△ABC三边的中点，若△ABC的周长是6cm，则△DEF的周长为
     
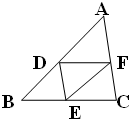
    ．精英家教网

    查看答案和解析>>

    点D、E、F分别是△ABC的边AB、BC、CA的中点．如图所示，若以BD、BE为边分别作正△BMD和正△BEN，连接MF、FN、MN． 易证△FMN是等边三角形，因而∠MFN=60°；若以BD、BE为边分别作正方形BPMD和正方形BQNE，连接MF、NF、MN，则∠MFN的度数是
    90°
    90°
    ；若以BD、BE为边分别作正n边形，设两个正n边形与点D、E相邻的顶点分别是M、N（点M、N与点B是不同的点），连接MF、NF、MN得到△FMN，则∠MFN的度数是
    180°-
    360°
    n
    180°-
    360°
    n
    ．

    查看答案和解析>>


    同步练习册答案