
题目列表(包括答案和解析)
如图1,在四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() 并延长,分别与
并延长,分别与![]() 的延长线交于点
的延长线交于点![]() ,则
,则![]() (不需证明).
(不需证明).
(温馨提示:在图1中,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,根据三角形中位线定理,证明
,根据三角形中位线定理,证明![]() ,从而
,从而![]() ,再利用平行线性质,可证得
,再利用平行线性质,可证得![]() .)
.)
问题一:如图2,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() ,分别交
,分别交![]() 于点
于点![]() ,判断
,判断![]() 的形状,请直接写出结论.
的形状,请直接写出结论.
问题二:如图3,在![]() 中,
中,![]() ,
,![]() 点在
点在![]() 上,
上,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() 并延长,与
并延长,与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,连结
,连结![]() ,判断
,判断![]() 的形状并证明.
的形状并证明.
 |
如图1,在四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() 并延长,分别与
并延长,分别与![]() 的延长线交于点
的延长线交于点![]() ,则
,则![]() (不需证明).
(不需证明).
(温馨提示:在图1中,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,根据三角形中位线定理,证明
,根据三角形中位线定理,证明![]() ,从而
,从而![]() ,再利用平行线性质,可证得
,再利用平行线性质,可证得![]() .)
.)
问题一:如图2,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() ,分别交
,分别交![]() 于点
于点![]() ,判断
,判断![]() 的形状,请直接写出结论.
的形状,请直接写出结论.
问题二:如图3,在![]() 中,
中,![]() ,
,![]() 点在
点在![]() 上,
上,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() 并延长,与
并延长,与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,连结
,连结![]() ,判断
,判断![]() 的形状并证明.
的形状并证明.
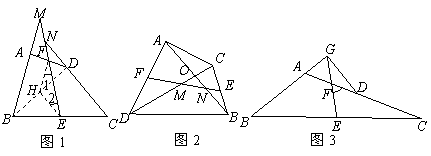
如图l,在四边形A8CD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,可证得HE=HF,从而∠HFE=∠HEF,再利用平行线的性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论.
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G, 若∠EFC=600,连结GD,判断△AGD的形状并证明.

如图,在四边形A8CD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,可证得HE=HF,从而∠HFE=∠HEF,再利用平行线的性质,可证得∠BME=∠CNE.)

问题一:如图,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论.
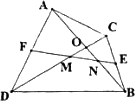
问题二:如图,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=600,连结GD,判断△AGD的形状并证明.

如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在下图中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)

问题一:如图,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论.

问题二:如图,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=60°,连结GD,判断△AGD的形状并证明.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com