
题目列表(包括答案和解析)
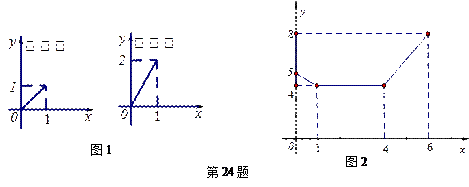
(本小题满分12分)
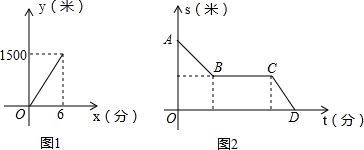
一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同. 进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x(单位:分)如图2所示.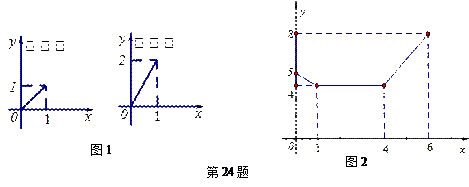
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
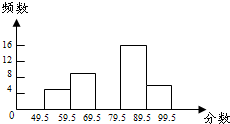 如图10所示的频数频数分布表和部分频数分布直方图.
如图10所示的频数频数分布表和部分频数分布直方图.| 分 数 段 | 频 数 | 频 率 |
| 49.5~59.5 | 5 | 0.1 |
| 59.5~69.5 | a | 0.18 |
| 69.5~79.5 | 14 | 0.28 |
| 79.5~89.5 | 16 | b |
| 89.5~99.5 | 6 | 0.12 |
| c |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com