
题目列表(包括答案和解析)
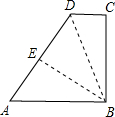 如图,在梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24,将该梯形折叠,点A恰好与点D重合,BE为折痕,那么AD的长度为
如图,在梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24,将该梯形折叠,点A恰好与点D重合,BE为折痕,那么AD的长度为 如图,在梯形ABCD中,AD∥BC,∠B=60°,∠ADC=105°,AD=6,且AC⊥AB,求AB的长.
如图,在梯形ABCD中,AD∥BC,∠B=60°,∠ADC=105°,AD=6,且AC⊥AB,求AB的长.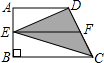 如图,直角梯形ABCD的中位线EF=a,垂直于底的腰AB=b,则图中阴影部分△ECD的面积为
如图,直角梯形ABCD的中位线EF=a,垂直于底的腰AB=b,则图中阴影部分△ECD的面积为 28、如下图,直角梯形ABCD中,AD∥BC,AD=24cm,BC=26cm,∠B=90°,动点P从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动、P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问t为何值时,(1)四边形PQCD是平行四边形.(2)当t为何值时,四边形PQCD为等腰梯形.
28、如下图,直角梯形ABCD中,AD∥BC,AD=24cm,BC=26cm,∠B=90°,动点P从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动、P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问t为何值时,(1)四边形PQCD是平行四边形.(2)当t为何值时,四边形PQCD为等腰梯形.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com