填空并完成推理过程．

　　　（1）如图（1），，（已知）

　　　　　　　　　　＝．(　　　　　　　　　　　　　　　)

　　　　　　，(已知)

　　　　　　＝　　　　　　，(　　　　　　　　　　　　　　)

　　　　　　＝　　　　　　；(　　　　　　　　　　　　　　　)

　　　（2）如图（2），已知，，．试判断与的关系，并说明你的理由．

　 解：，理由是：，．(已知)

　　　　　　　　　　　　＝　　　　　＝．(　　　　　　　　)

　　　　　　　，(　　　　　　　　)

　　　　　　　，即．

　　　　　　　　　　　　　　　　　　；(　　　　　　　　　　　　　　　　

(3) 如图(3)，点为上的点，点为上的点，，，试说明：．

　　解：，(已知)，(　　　　　　　　　　　　　)

　　　　　　，(等量代换)

　　　　　　　　　　　　，(　　　　　　　　　　　　　　　　　　　　)

　　　　，(　　　　　　　　　　　　　　　　　　　　　)

　　　　又，(已知)

　　　　，(　　　　　　　　　　　　　)

　　　　．(　　　　　　　　　　　　　　　　　　　　　　　　　　　)

阅读下列证明过程：已知，如图四边形ABCD中，AB＝DC，AC＝BD，AD≠BC，求证：四边形ABCD是等腰梯形．

读后完成下列各小题．

(1)证明过程是否有错误？如有，错在第几步上，答：　　　　　　　　　　　　 　　　　　　　　　　　　 ．

(2)作DE∥AB的目的是：　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　 ．

(3)有人认为第9步是多余的，你的看法呢？为什么？答：　　　　　　　　　　　　　　 　　　　　　　　　　　　　　．

(4)判断四边形ABED为平行四边形的依据是：　　　　　　　　　　　　 　　　　　　　　　　 ．

(5)判断四边形ABCD是等腰梯形的依据是　　　　　　　　　　　　 　　　　　　　　　　　　．

(6)若题设中没有AD≠BC，那么四边形ABCD一定是等腰梯形吗？为什么？

答：　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　 ．

2011年3月16日上午10时福岛第一核电站第3号反应堆发生了爆炸。为了抑制核辐射进一步扩散，日本决定向6号反应堆注水冷却，铀棒被放在底面积为100m²、高为20m的长方体水槽中的一个圆柱体桶内，如图（1）所示，向桶内注入流量一定的水，注满后，继续注水，直至注满水槽为止（假设圆柱体桶在水槽中的位置始终不改变）。水槽中水面上升的高度h与注水时间t之间的函数关系如图（2）所示。

(1)求圆柱体的底面积；(2)若的圆柱体高为9m，求注水的速度及注满水槽所用时间。

　　　　　　　　　　　　　　　 h(cm)

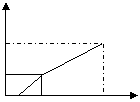
　　　　　　　　　　　　　 O 18 90 20　　　　 t(s)　　　　　　　　　　　　　　　　　　　　　　　　

A  B    C   D

　　　　　　　　　　　　　　　　　　　　　　　　　　　　    A

　　　　　　　　　　　　　　　　　　　　　　　　　　    D　　 E

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B 　　  C 　　

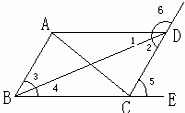
如图，∠5=∠CDA =∠ABC，∠1=∠4，∠2=∠3，∠BAD+∠CDA=180°，填空：

∵∠5=∠CDA（已知）

∴　　 //　　 (　　　　　　　　　　 ）　　　　　　　　　　　　　　

∵∠5=∠ABC（已知）

∴　　 //　　 (　　　　　　　　　　 ）　　　　　　　　　　　　　　

∵∠2=∠3（已知）

∴　　 //　　 (　　　　　　　　　　　　）　　　　　　　　　　　　　　　　

∵∠BAD+∠CDA=180°（已知）

∴　　 //　　 (　　　　　　　　　　　　 ）

∵∠5=∠CDA（已知），又∵∠5与∠BCD互补（　　　　　　　　　　　　　　）

∠CDA与　　　　 互补（邻补角定义）

∴∠BCD=∠6（　　　　　　　　　　　　）

∴　　 //　　　　(　　　　　　　　　　　　　　 ）