
题目列表(包括答案和解析)

探究与思考:(①题每空1分,②题每空2分,共12分)
①现定义某种运算“*”,对任意两个有理数a、b,有a*b=ab,如(-3)*2= =9.
=9.
试计算: ( - )*2 = , (-1)*(2*3)= .
)*2 = , (-1)*(2*3)= .
②现有若干个数,第1个数记为 ,第二个数记为
,第二个数记为 ,第三个数记为
,第三个数记为 ……,第n个数记为
……,第n个数记为 ,若
,若 ,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。”
,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。”
(1)试计算
(2)根据以上结果,请你写出 ,
,

某商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件。设这种商品的销售单价为x元,商品每天销售这种商品所获得的利润为y元.
(1)给定x的一些值,请计算y的一些值.(每空1分,共4分)
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | 320 | | | | | … |
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | 320 | 420 | 480 | 500 | 480 | … |
(本题14分)如图,在平面直角坐标系中.四边形OABC是平行四边形.直线![]() 经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(
经过O、C两点.点A的坐标为(8,o),点B的坐标为(11.4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C—B相交于点M。当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P、Q运动的时间为t秒(![]() ).△MPQ的面积为S.
).△MPQ的面积为S.
(1)点C的坐标为___________,直线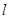 的解析式为___________.(每空l分,共2分)
的解析式为___________.(每空l分,共2分)
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围。
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值。
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线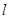 相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
相交于点N。试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com