若a、b 是正数，且满足，则a与b的大小关系是（    ）

A、             B、                 C、            D、不能确定

A、8	B、8或-1
C、2或-1	D、8或-1

甲、乙两位采购员同去一家饲料公司购买了两次饲料．两次的饲料的价格有变化，而两位采购员的购货方式也不同，其中，采购员甲每次购买1000kg，采购员乙每次用去800元钱，而不管买多少饲料．若两次购买饲料的单价分别为m元/kg和n元/kg（m，n是正数，且m≠n），
（1）用含m，n的代数式表示：甲两次购买共付款元，乙两次购买kg饲料；甲两次购买饲料的平均单价元/kg，乙两次购买饲料的平均单价元/kg．
（2）若规定谁两次购饲料的平均价格低，谁的方式就合理，请你判断一下哪一个合理？说明理由．

问题提出
我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一．所谓“作差法”：就是通过作差、变形，并利用差的符号确定它们的大小，即要比较代数式M、N的大小，只要作出它们的差M-N，若M-N＞0，则M＞N；若M-N=0，则M=N；若M-N＜0，则M＜N．
问题解决
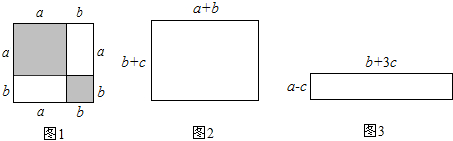
如图1，把边长为a+b（a≠b）的大正方形分割成两个边长分别是a、b的小正方形及两个矩形，试比较两个小正方形面积之和M与两个矩形面积之和N的大小．
解：由图可知：M=a²+b²，N=2ab．
∴M-N=a²+b²-2ab=（a-b）²．
∵a≠b，∴（a-b）²＞0．
∴M-N＞0．
∴M＞N．
类比应用
（1）已知小丽和小颖购买同一种商品的平均价格分别为

a+b

2

元/千克和

2ab

a+b

元/千克（a、b是正数，且a≠b），试比较小丽和小颖所购买商品的平均价格的高低．
（2）试比较图2和图3中两个矩形周长M₁、N₁的大小（b＞c）．

联系拓广
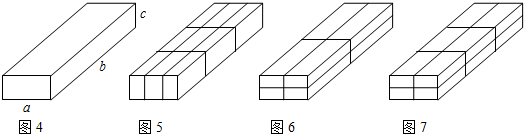
小刚在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图4所示（其中b＞a＞c＞0），售货员分别可按图5、图6、图7三种方法进行捆绑，问哪种方法用绳最短？哪种方法用绳最长？请说明理由．