
题目列表(包括答案和解析)
阅读下列材料:
小明遇到一个问题:已知:如图1,在△ABC中,∠BAC=120°,∠ABC=40°,试过△ABC的一个顶点画一条直线,将此三角形分割成两个等腰三角形.
他的做法是:如图2,首先保留最小角∠C,然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角,使∠DAC=20°,△ABC即可被分割成两个等腰三角形.
喜欢动脑筋的小明又继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
他的做法是:



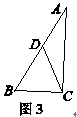
如图3,先画△ADC ,使DA=DC,延长AD到点B,使△BCD也是等腰三角形,如果DC=BC,那么∠CDB =∠ABC,因为∠CDB=2∠A,所以∠ABC= 2∠A.于是小明得到了一个结论:
当三角形中有一个角是最小角的2倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
请你参考小明的做法继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请直接写出你所探究出的另外两条结论(不必写出探究过程或理由).


阅读下列材料:
小明遇到一个问题:已知:如图1,在△ABC中,∠BAC=120°,∠ABC=40°,试过△ABC的一个顶点画一条直线,将此三角形分割成两个等腰三角形.
他的做法是:如图2,首先保留最小角∠C,然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角,使∠DAC=20°,△ABC即可被分割成两个等腰三角形.
喜欢动脑筋的小明又继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
他的做法是:


如图3,先画△ADC ,使DA=DC,延长AD到点B,使△BCD也是等腰三角形,如果DC=BC,那么∠CDB =∠ABC,因为∠CDB=2∠A,所以∠ABC= 2∠A.于是小明得到了一个结论:
当三角形中有一个角是最小角的2倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
请你参考小明的做法继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请直接写出你所探究出的另外两条结论(不必写出探究过程或理由).
阅读下列材料:
小明遇到一个问题:已知:如图1,在△ABC中,∠BAC=120°,∠ABC=40°,试过△ABC的一个顶点画一条直线,将此三角形分割成两个等腰三角形.
他的做法是:如图2,首先保留最小角∠C,然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角,使∠DAC=20°,△ABC即可被分割成两个等腰三角形.
喜欢动脑筋的小明又继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
他的做法是:



如图3,先画△ADC ,使DA=DC,延长AD到点B,使△BCD也是等腰三角形,如果DC=BC,那么∠CDB =∠ABC,因为∠CDB=2∠A,所以∠ABC= 2∠A.于是小明得到了一个结论:
当三角形中有一个角是最小角的2倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
请你参考小明的做法继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请直接写出你所探究出的另外两条结论(不必写出探究过程或理由).
 13、探究题:
13、探究题:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com