
题目列表(包括答案和解析)
如图,过点B(2,0)的直线l:![]() 交y轴于点A,与反比例函数
交y轴于点A,与反比例函数![]() 的图象交于点C(3,n).、
的图象交于点C(3,n).、

(1)求反比例函数的解析式;
(2)将△OBC绕点O逆时针方向旋转α角(α为锐角),
得到△OB′C′.当OC′⊥AB时,求点C运动的路径长.
【解析】(1)由点B求出直线l的解析式,从而求得n的值,解出反比例函数的解析式,(2)当OC′⊥AB时,α=60°,由勾股定理求出OC长,从而![]() 的长度
的长度
(本题满分8分)已知![]() 在平面直角坐标系中的位置如下图所示.(1)分别写出图中点
在平面直角坐标系中的位置如下图所示.(1)分别写出图中点![]() 的坐标;(2)画出
的坐标;(2)画出![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 后的
后的![]() ;(3)求点
;(3)求点![]() 旋转到点
旋转到点![]() 所经过的路线长(结果保留
所经过的路线长(结果保留![]() ).
).
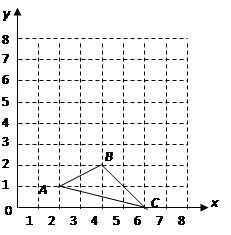
【解析】(1)在直角坐标系中读出A的坐标,点C的坐标;
(2)根据旋转的性质画出△ABC绕点A按逆时针方向旋转90°后的△A′B′C′;
(3)先根据勾股定理求出AC的长,然后利用弧长的计算公式求解即可
如图,过点B(2,0)的直线l: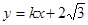 交y轴于点A,与反比例函数
交y轴于点A,与反比例函数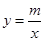 的图象交于点C(3,n).、
的图象交于点C(3,n).、
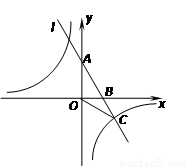
(1)求反比例函数的解析式;
(2)将△OBC绕点O逆时针方向旋转α角(α为锐角),
得到△OB′C′.当OC′⊥AB时,求点C运动的路径长.
【解析】(1)由点B求出直线l的解析式,从而求得n的值,解出反比例函数的解析式,(2)当OC′⊥AB时,α=60°,由勾股定理求出OC长,从而 的长度
的长度
一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
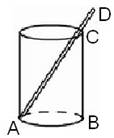
【解析】由于吸管、圆柱形杯内部底面直径与杯壁正好构成直角三角形,故可先利用勾股定理求出AB的长,进而可得出结论
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com