
题目列表(包括答案和解析)
如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段DE由BC出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM,设运动时间为t秒(0<t<8).
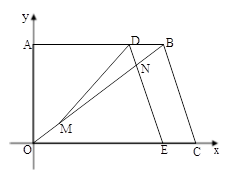
(1) 当![]() 为何值时,DM∥OA?
为何值时,DM∥OA?
(2)连接ME,在点M、N重合之前的运动过程中,五边形DMECB的面积是否发生变化?若不变,请求出它的值;若发生变化,请说明理由.
(3)当t为何值时,△DMB为等腰三角形.
【解析】(1) 首先用t表示出BD、BM的长,若DM∥OA, 根据比例线段求出t的值
(2)易求得OB=OC=10,即可知BM=OE=10-t,而BD=OM=t,且∠DBM=∠MOE,即可证得△BDM≌△OME,因此五边形的面积可转化为△OBC的面积,因此五边形的面积是定值,以OC为底、OA为高,即可求得△OCB的面积,也就是这个定值的大小
(3)根据BD=BM,BD=DM,BM=MD三种情况分析,
如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段DE由BC出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM,设运动时间为t秒(0<t<8).
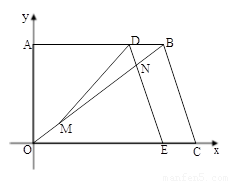
(1) 当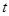 为何值时,DM∥OA?
为何值时,DM∥OA?
(2)连接ME,在点M、N重合之前的运动过程中,五边形DMECB的面积是否发生变化?若不变,请求出它的值;若发生变化,请说明理由.
(3)当t为何值时,△DMB为等腰三角形.
【解析】(1) 首先用t表示出BD、BM的长,若DM∥OA, 根据比例线段求出t的值
(2)易求得OB=OC=10,即可知BM=OE=10-t,而BD=OM=t,且∠DBM=∠MOE,即可证得△BDM≌△OME,因此五边形的面积可转化为△OBC的面积,因此五边形的面积是定值,以OC为底、OA为高,即可求得△OCB的面积,也就是这个定值的大小
(3)根据BD=BM,BD=DM,BM=MD三种情况分析,
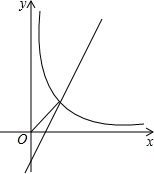 已知一次函数y=kx+b(k≠0)和反比例函数y=
已知一次函数y=kx+b(k≠0)和反比例函数y=| k | 2x |
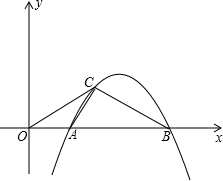
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com