
题目列表(包括答案和解析)
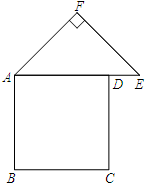 (2012•和平区一模)如图,有一张纸片,是由边长为a的正方形ABCD、斜边长为2b的等腰直角三角形FAE组成的(b<a),∠AFE=90°,且边AD和AE在同一条直线上.要通过适当的剪拼,得到一个与之面积相等的正方形.
(2012•和平区一模)如图,有一张纸片,是由边长为a的正方形ABCD、斜边长为2b的等腰直角三角形FAE组成的(b<a),∠AFE=90°,且边AD和AE在同一条直线上.要通过适当的剪拼,得到一个与之面积相等的正方形.| a2+b2 |
| a2+b2 |
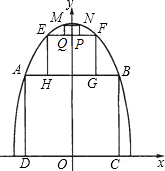 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: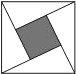 (2013•平遥县模拟)“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).随机在大正方形及其内部区域投针,若针扎到小正方形(阴影部分)的概率是
(2013•平遥县模拟)“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).随机在大正方形及其内部区域投针,若针扎到小正方形(阴影部分)的概率是| 1 |
| 9 |
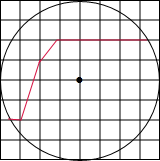 如图所示,圆被一条折线(图中粗线)所分成的两部分面积之差为
如图所示,圆被一条折线(图中粗线)所分成的两部分面积之差为| 1 |
| 2 |
| 1 |
| 2 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com