
题目列表(包括答案和解析)
| 1 | 3 |
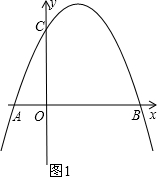
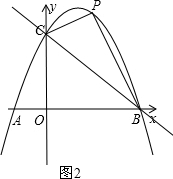
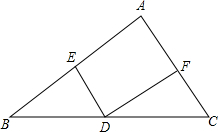
 (2013•潍坊)为了改善市民的生活环境,我市在某河滨空地处修建一个如图所示的休闲文化广场,在Rt△ABC内修建矩形水池DEFG,使定点D,E在斜边AB上,F,G分别在直角边
(2013•潍坊)为了改善市民的生活环境,我市在某河滨空地处修建一个如图所示的休闲文化广场,在Rt△ABC内修建矩形水池DEFG,使定点D,E在斜边AB上,F,G分别在直角边| 3 |
| 1 |
| 3 |
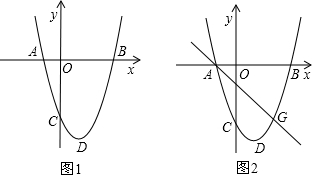
 交AC于F,已知BC=5,S△ABC=S.
交AC于F,已知BC=5,S△ABC=S.| 2 | 5 |
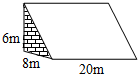 如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com