
题目列表(包括答案和解析)
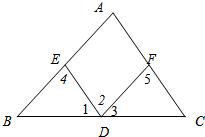 25、如图,
25、如图,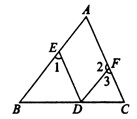
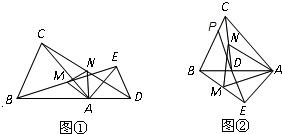 25、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
25、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺
规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).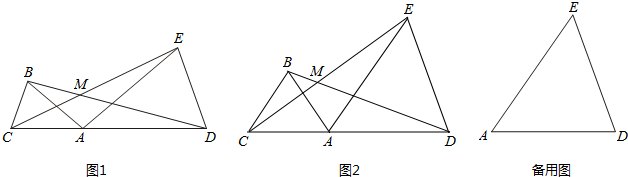
已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
(2)如图2,若AB=BC=kAC,AD=ED=kAE,则线段BD与CE的数量关系为 _________ ,∠BMC= _________ (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接EC并延长交BD于点M.则∠BMC= _________ (用α表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com