
题目列表(包括答案和解析)
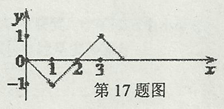
如图(1),Rt ∆ABC中,![]() 垂足为D.AF平分∠CAB.交CD于点E,交CB于点F.
垂足为D.AF平分∠CAB.交CD于点E,交CB于点F.
1.求证:CE=CF;
2.将图(1)中的∆ADE沿AB向右平移到∆A'D'E'的位置,使点E’落在BC边上,其它条件不变,如图(2)所示.试猜想:BE’与CF有怎样的数量关系?请证明你的结论.
如图(1),Rt ∆ABC中,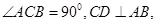 垂足为D.AF平分∠CAB.交CD于点E,交CB于点F.
垂足为D.AF平分∠CAB.交CD于点E,交CB于点F.
1.求证:CE=CF;
2.将图(1)中的∆ADE沿AB向右平移到∆A'D'E'的位置,使点E’落在BC边上,其它条件不变,如图(2)所示.试猜想:BE’与CF有怎样的数量关系?请证明你的结论.
 解得
解得


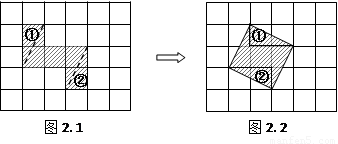
如图2.1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2.2所示的正方形,那么所拼成的正方形的边长为
A. 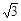 B. 2
C.
B. 2
C. 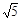 D.
D. 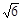
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com