如图，已知一次函数y =  -  x +7与正比例函数y  =   x的图象交于点A，且与x轴交于点B.

（1）求点A和点B的坐标；

（2）过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从原点O出发，以每秒1个单位长的速度，沿O—C—A的路线向点A运动；同时直线l从点B出发，以相同速度沿x轴向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒.

①当t为何值时，以A、P、R为顶点的三角形的面积为8？

②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若不存在，请说明理由． （2011江苏盐城第28题改编）

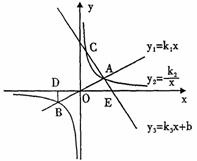
如图，正比例函数与反比例函数相交于A、B点，已知点A的坐标为（4，n），BD⊥x轴于点D，且S_△BDO=4。过点A的一次函数与反比例函数的图像交于另一点C，与x轴交于点E（5，0）。

（1）求正比例函数、反比例函数和一次函数的解析式；

（2）结合图像，求出当时x的取值范围。

         第26题

今年我国多个省市遭受严重干旱，受旱灾的影响，4月份，我市某蔬菜价格呈上升趋势，其前四周每周的平均销售价格变化如下表：

周数x	1	2	3	4
价格y（元/kg）	2	2.2	2.4	2.6

进入5月，由于本地蔬菜的上市，此种蔬菜的平均销售价格y（元/千克）从5月第1周的2.8元/千克下降至第2周的2.4元/千克，且y与周数x的变化情况满足二次函数y=-

1

20

x²+bx+c．
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式，并求出5月份y与x的函数关系式；
（2）若4月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m=

1

4

x+1.2，5月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m=-

1

5

x+2．试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大？且最大利润分别是多少？
（3）若5月份的第2周共销售100吨此种蔬菜．从5月份的第3周起，由于受暴雨的影响，此种蔬菜的可供销量将在第2周销量的基础上每周减少a%，政府为稳定蔬菜价格，从外地调运2吨此种蔬菜，刚好满足本地市民的需要，且使此种蔬菜的销售价格比第2周仅上涨0.8a%．若在这一举措下，此种蔬菜在第3周的总销售额与第2周刚好持平，请你参考以下数据，通过计算估算出a的整数值．
（参考数据：37²=1369，38²=1444，39²=1521，40²=1600，41²=1681）

现在互联网越来越普及，网上购物的人也越来越多，订购的商品往往通过快递送达．当当网上某“四皇冠”级店铺率先与“青蛙王子”童装厂取得联系，经营该厂家某种型号的童装．根据第一周的销售记录，该型号服装每天的售价x（元/件）与当日的销售量y（件）的相关数据如下表：

每件的销售价x（元/件）	200	190	180	170	160	150	140
每天的销售量y（件）	80	90	100	110	120	130	140

已知该型号童装每件的进价是70元，同时为吸引顾客，该店铺承诺，每件服装的快递费10元由卖家承担．
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求第一周销售中，y与x的函数关系式；
（2）设第一周每天的赢利为w元，求w关于x的函数关系式，并求出每天的售价为多少元时，每天的赢利最大？最大赢利是多少？
（3）从第二周起，该店铺一直按第（2）中的最大日盈利的售价进行销售．但进入第三周后，网上其他购物店也陆续推出该型号童装，因此第三、四周该店铺每天的售价都比第二周下降了m%，销售量也比第二周下降了0.5m%（m＜20）；第五周开始，厂家给予该店铺优惠，每件的进价降低了16元；该店铺在维持第三、四周的销售价和销售量的基础上，同时决定每件童装的快递费由买家自付，这样，第五周的赢利相比第二周的赢利增加了2%，请估算整数m的值．
（参考数据：

5.601

≈2.37，

56.01

≈7.49）