练习册

  • 练习册
  • 试题
    1旋转(1) 第1题. 如图所示的图案.它可以看成是什么“基本图案 通过怎样的放置而得到到的? 答案:解:图案是以一个叶片和柄为“基本图案 .通过连续四次旋转而形成. 旋转解度分别等于． 第2题. 如图可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度? 答案:解:一个菱形旋转5次得到的.旋转的角度分别为:． 第3题. 如图.你能分析出图中的旋转现象吗? 答案:解:整个图形可以看做是图形的六分之一绕中心位置.按同一方向连续旋转前后的图形共同组成的, 也可以看做是图形的三分之一绕中心位置.按同一方向旋转前后的图形共同组成的, 也可以看做是图形的二分之一绕中心位置旋转前后的图形共同组成的, 还可以看做是矩形绕中心位置分别旋转前后的图形共同组成的． 第4题. 如图.可以看做是由一个三角形旋转而成的.它一共旋转 次.分别旋转 度而形成的． 答案:8 第5题. 如图.整个圆形可以看做是图形的 绕中心位置.按照同一方向连续旋转 前后的图形共同组成的.也可以看做是图形的 绕中心位置连续旋转 前后的图形共同组成的．还可以看做图形的 绕中心旋转 前后的图形共同组成的． 答案:八分之一 四分之一 二分之一 第6题. 如图.在正方形中.是的中点.是延长线上一点.．问:(1)可以通过平移.翻折.旋转中的哪种方法.使变到的位置?(2)指出图中线段与之间的关系． 答案:(1)绕点逆时针旋转,(2)相等． 第7题. 如图.下列四个图形都可以分别看做由一个“基本图案 经过旋转所形成.则它们中旋转角相同的图形为( ) A． C． 答案:D 第8题. 如图.矩形的边长.若矩形以为中心.按顺时针方向旋转到的位置(点落在对角线上).则的形状为( ) A．等腰三角形 B．等边三角形 C．等腰直角三角形 D．无法确定 答案:B 第9题. 如图所示.钟表的分针匀速旋转一周需要60分.在这个问题中. (1)旋转中心是 ． (2)现在钟面上是2点.如果过10min.那么分针旋转了 度.时针旋转了 度． (3)如果再经过15min.那么分针共旋转了 度.时针共旋转了 度． 答案:60 5 (3) 第10题. 如图.在中..以直角顶点为旋转中心.将旋转到的位置.其中分别是的对应点.且点在斜边上.交于 ． 答案: 第11题. 钟表的分针旋转一周需要60分钟.时针旋转一周需要12小时.秒针旋转一周需要60秒则1小时时针旋转 度.分针旋转 度.秒针旋转 度.经过900秒.时针旋转 度.分针旋转 度.钞针旋转 度． 答案: 第12题. 记得雪花的样子吗?它可以看作是由什么“基本图案 通过怎样的变化得到的? 答案:略 第13题. 九点20分时.时针和分针的夹角是多少度? 答案: 第14题. 如图.是否存在这样的两个三角形.其中一个是另一个通过旋转得到的?旋转多大角度?并进一步分析此图案的构成? 答案:存在 旋转 第15题. 请分析下图中的旋转现象． 答案:可以看成由图形的六分之一绕中心位置按同一方向连续旋转.前后的图形共同组成． 第16题. 如图.图中所有的小三角形均是全等的等边三角形.其中的菱形可以看成是把菱形以为中心( ) A．顺时针旋转得到 B．顺时针旋转得到 C．逆时针旋转得到 D．逆时针旋转得到 答案:D 第17题. 在图形旋转中.下列说法中错误的是( ) A．图形上的每一点到旋转中心的距离相等 B．图形上的每一点转动的角度相同 C．图形上可能存在不动点 D．图形上任意两点的连线与其对应两点的连线相等 答案:A 第18题. 在平面内.将一个图形沿 .移动 .这种图形运动叫平移．在平面内.将一个图形绕 .沿 转动 .这种图形运动叫旋转．平移.旋转只改变图形 .不改变图形的 和 ． 答案:一定的方向.一定的距离.某一个定点.一定的方向.一个角度.位置.大小.形状 第19题. 如图所示.如果四边形旋转后能与正方形重合.则图形所在的平面上可以作为旋转中心的点有多少个? 答案:解:观察图形.绕点顺时针旋转或绕点逆时针旋转都可以与正方形重合,且绕的中点旋转也可以与正方形重合．因此可作为旋转中心的点有3个.分别是点.点和点． 第20题. 如图.为等腰直角三角形.而是由按顺时针方向旋转而来的.如果.试问:(1)是由旋转多少度得到的?旋转中心在哪里?(2)为多少度?(3)图中有哪几个全等三角形? 答案:解:(1)易知为旋转中心.由于是的旋转而得. 故是由按顺时针旋转得到的． (2) 为等腰直角三角形形． ． 又旋转不改变图形形状和大小． 从而． (3)在和中. ． ． 又由旋转而来． ． 第21题. 如图.在五边形中.．试说明平分的理由． 答案:解:如图.连结.将绕点旋转的度数到的位置. 因为.所以与重合． 因为.且. 所以. 所以三点在一条直线上.． 在与中.． 又.所以． 因此即平分． 第22题. 如图.是直角三角形.是斜边.将绕点逆时针旋转后.能与重合．如果.求的长． 答案:解:绕点逆时针旋转后.能与重合. 为等腰直角三角形.为斜边． ． 第23题. 如图.为等腰直角三角形.其中为高,以为旋转中心将逆时针旋转后构成新图形.试问此图形是什么? 答案:解:如图.为等腰三角形. .旋转后点与点重合． . ． 点在一条直线上． 又. 为等腰直角三角形． 第24题. 如图.把直角三角形的斜边放在定直线上.按顺时针方向在上转动两次.使它转到的位置．设.则顶点运动到点的位置时.点经过的路线与直线所围成的面积是多少? 答案:解:由条件易知． 第一次以为旋转中心点所经过的路线与直线所围成的面积为 , 第二次以为旋转中心点所经过的路线与直线所围成的面积为 ． 总面积为． 第25题. 经过旋转.图形上的每一点都绕 沿相同 转动了相同的 .任意一对对应点与旋转中心的连线所成的角都是 .对应点到 的距离相等． 答案:旋转中心 方向 角度 旋转角 旋转中心 第26题. 如图.它是由一个花瓣旋转 次.分别旋转 而得到的． 答案:3 第27题. 如图所示.为一个风车的图形.其中一个图形是否为另一个图形经过旋转得来的? 答案:解:(1)可由图形①旋转前后的图形构成, (2)可由图形②旋转前后的图形构成, (3)可由图形③旋转前后的图形构成． 第28题. 如图.中..中线.是由旋转所得.则边的取值范围是( ) A． B． C． D． 答案:D 第29题. 如图所示.绕旋转中心旋转.到.那么 (1)点的对应点是点 ． (2)点的对就点是点 ． (3)线段的对应线段是线段 ． (4)线段的对应线段是线段 ． (5)线段的对应线段是线段 ． (6)的对应角是 ． (7)的对应角是 ． (8)的对应角是 ． 答案:(1) (2) (3) (4) (5) (6)(7) (8) 第30题. 如图.在下边的各组图案中.请你说出位置变化的名称． (1)到的位置变换叫做 ． (2)到的位置变换叫做 ． (3)和的位置变换叫做 ． 答案:轴对称 (3)旋转 第31题. 如图.是一个五叶风车的示意图.它可以看做是由“基本图案 通过 次旋转而得,若该风车在风中匀速旋转一周需s.则经过s.一个三角形叶片旋转了 度． 答案:一个三角形 5 72 第32题. 如图.和是等腰直角三角形.和是直角.则图中可通过旋转而相互得到三角形是 ,旋转角为 度.旋转中心为 .写出所有的对应线段 .由此可知线段与的位置关系为 ． 答案:与.90...垂直 第33题. 已知.将绕平面内一点旋转得到.则的度数为 ． 答案: 第34题. 正六边形可以看作是 形通过 次旋转图形.每次旋转 度.旋转方向是 ． 答案:正三角形.5..逆时针或顺时针 第35题. 如图.和都是等边三角形.图中的三角形中.哪些三角形可以通过互相旋转得到? 答案: 第36题. 如图.转盘上有“ 6个等格． ①如果转盘顺时针旋转.字母“ 旋转 度时.才能得到字母“ 的位置.字母“ 旋转 度时.才能转到字母 “ 的位置． ②如果转盘逆时针旋转.字母“ 旋转 度时.才能转到字母“ 的位置． 答案:① ② 第37题. 在五边形中.． 求证:平分． 答案:解:连结.将绕点旋转的度数到的位置． 因为. 所以与重合. 因为.且. 所以. 所以三点共交.. 在和中. (SSS)． ． 第38题. 如图的边绕点旋转到的位置.则下列说法正确的是( ) A．点与点是对应点.则． B． C． D．线段与线段是对应线段 答案:C 第39题. 将如图所示的图案绕其中心旋转时与原图案完全重合.那么的最小值是( ) A．60 B．90 C．120 D．180 答案:C 【查看更多】

     

    题目列表(包括答案和解析)

    以下两题请选择一题解答，若两题都答，只把第1题的分数记入学分．
    ①如图1，已知射线OC在平角∠AOB的内部，且∠AOC＞∠BOC，OD平分∠AOC，OE平分∠BOC．
    （1）比较∠COD与∠COE的大小，并说明理由．
    （2）你能求出∠DOE的大小吗？如果能，请求出它的度数，若不能，说明理由．
    （3）若∠AOB=a，你能用a表示∠DOE的度数吗？请说明理由．
    ②如图2，∠AOC与∠BOD都是直角，∠BOC=50°．
    （1）求∠AOB和∠DOC的度数，∠AOB和∠DOC有何大小关系？
    （2）若∠BOC的具体度数不稳定，其他条件不变，这种关系仍然成立吗？说明理由．
    （3）试猜想∠AOD与∠COB在数量上是相等、互余，还是互补关系？你能用推理的方法说明你的猜想是否合理吗？
    （4）当∠BOD绕点O旋转到图3位置时，你原来的猜想还成立吗？说明理由．

    查看答案和解析>>

    课本习题研究：
    （1）课本116页第12题题目内容是这样的：正方形ABCD的对角线交于点O，点O又是另一个正方形A′B′C′O的一个顶点．如果两个正方形的边长相等，那么正方形A′B′C′O绕点O无论怎样旋转，两个正方形重叠部分的面积，总等于一个正方形面积的
     
    ．请你根据对课本习题的研究，填写（2）题的答案．
    （2）如图，将n个边长都为1cm的正方形按如图所示摆放，点A1、A2、…、An，分别是正方形的中心，则n个这样的正方形重叠部分的面积和为
     
    cm2．
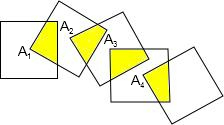
    精英家教网

    查看答案和解析>>

    精英家教网附加题：对于本试卷第19题：“图中△ABC外接圆的圆心坐标是”．请再求：
    （1）该圆圆心到弦AC的距离；
    （2）以BC为旋转轴，将△ABC旋转一周所得几何体的全面积．（所有表面面积之和）

    查看答案和解析>>

    如图所示，在平面直角坐标系xOy中，正方形的边长为1，将其沿轴的正方向连续滚动，即先以顶点A为旋转中心将正方形顺时针旋转90°得到第二个正方形，再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形，依此方法继续滚动下去得到第四个正方形，…，第n个正方形．设滚动过程中的点P的坐标为．

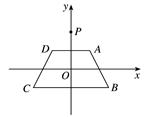
    【小题1】（1）画出第三个和第四个正方形的位置，并直接写出第三个正方形中的点P的坐标；
    【小题2】（2）画出点运动的曲线（0≤≤4），并直接写出该曲线与轴所围成区域的面积．

    查看答案和解析>>

    如图，在平面直角坐标系xOy中，等腰梯形ABCD的顶点坐标分别为A（1，1），B（2，－1），C（－2，－1），D（－1，1）．y轴上一点P（0，2）绕点A旋转180°得点P1，点P1绕点B旋转180°得点P2，点P2绕点C旋转180°得点P3，点P3绕点D旋转180°得点P4，……，重复操作依次得到点P1，P2，…， 则点P2010的坐标是（    ）．                  

    （第5题）

     
    A．（2010，2）B．（2010，）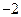

    		C．（2012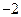，）D．（0，2）

    查看答案和解析>>


    同步练习册答案