方程中.⊿= .根的情况是 ,——青夏教育精英家教网—

方程中.⊿= .根的情况是 , 【查看更多】

题目列表(包括答案和解析)

方程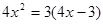中，⊿= ，根的情况是；

列方程解应用题：
为了鼓励居民节约用电，某地区规定：如果每户居民一个月的用电量不超过a度时，每度电按0.40元交费；如果每户居民一个月的用电量超出a度时，则该户居民的电费将使用二级电费计费方式，即其中有a度仍按每度电0.40元交费，超出a度部分则按每度电

元交费。下表是该地区一户居民10月份、11月份的用电情况。根据表中的数据，求在该地区规定的电费计费方式中，a度用电量为多少？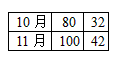

列方程或方程组解应用题：

在社会实践活动中，某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数)，三位同学汇报高峰时段的车流量情况如下：

甲同学说：“二环路车流量为每小时10000辆”；

乙同学说：“四环路比三环路车流量为每小时多2000辆”；

丙同学说：“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”．

请你根据他们所提供的信息，求出高峰时段三环路、四环路的车流量各是多少．

在△ABC中，a，b，c分别为∠A，∠B，∠C所对的边，我们称关于x的一元二次方程ax²+bx-c=0为“△ABC的☆方程”．根据规定解答下列问题：
（1）“△ABC的☆方程”ax²+bx-c=0的根的情况是

②

（填序号）：①有两个相等的实数根；②有两个不相等的实数根；③没有实数根；
（2）如图，AD为⊙O的直径，BC为弦，BC⊥AD于E，∠DBC=30°，求“△ABC的☆方程”ax²+bx-c=0的解；
（3）若x=

c是“△ABC的☆方程”ax²+bx-c=0的一个根，其中a，b，c均为整数，且ac-4b＜0，求方程的另一个根．

聪聪的爸爸是供电公司的线路设计师，公司准备在输电主干线l上连接一个分支线路，为新建的两个小区M、N同时输电．聪聪的爸爸设想了两种情况：①当小区M、N分别位于主干线l的两侧时，如图(一)；②当小区M、N分别位于主干线l的同侧时，如图(二)；

1.如果是图(一)的情况，请你帮助聪聪的爸爸设计，分支线路连接点P在什么地方时分支线路最短，并在图(一)中标出点P的位置.(保留作图痕迹)

2.如果是图二的情况，假设两小区相距2公里，M、N小区分别到主干线l的距离分别为2公里和1公里，请你帮助聪聪的爸爸计算一下分支线路最短的长度是▲公里.（结果保留根号）

3.经过实地考察测量，情况比设想的复杂．如图（三）所示，此段的主干线l在一段河堤AB上，河堤AB与CD平行，河宽0.5公里，小区M到河堤AB的距离为2公里，小区N到河堤CD的距离为1公里，两小区M、N的连线与主干线l所夹锐角恰好为45°，并且根据架线要求，当线路通过河道时，要求线路与河堤垂直．

①请你帮助聪聪的爸爸设计出最短的分支线路，并画出示意图．(要求：标注字母，保留痕迹，用字母说明具体线路)

②根据所画示意图计算最短线路有多长？（要求：写出计算过程，结果保留根号）

同步练习册答案