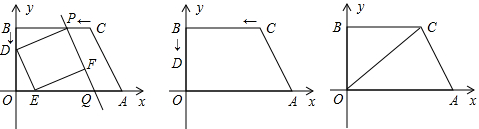
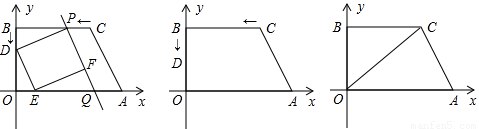
在平面直角坐标系内,已知点A和C的坐标分别为(8,0)和(5,4),过点C作CB⊥y轴于点B,点D从B出发,以每秒1个单位的速度延BO向终点O运动,点P从C出发,以每秒a(0<a≤1.25)个单位的速度延CB向终点B运动(当D点到达O点,P点也随之停止).过D作DE∥AC交OA于点E,过P作PQ∥AC交OA于点,连接PD,再过E作EF∥PD交PQ于F.设P、D两点的运动时间为t.
(1)分别求过A、C两点的直线和过B、C、A三点的抛物线的解析式;
(2)若a=1,求t为何值时,四边形DEFP为矩形?并求出此时直线PQ的解析式;
(3)是否存在这样的a,t的值,使四边形DEFP为正方形?若存在,求出此时a,t的值和正方形的面积;若不存在,说明理由;
(4)以A、O、C为顶点的△AOC中,M是AC上一动点,过M作MN∥OA交OC于N,试问,在x轴上是否存在点R,使得△MNR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.