
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 24 |
| 1 |
| 28 |
| 1 |
| 215 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 102 |
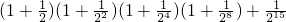 ;
;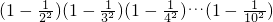 .
.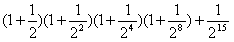 ;
;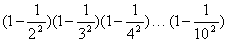 。
。在多项式:x2+4y2,-x2+y2,-a2-b2,a2+(-b2),8x2-9,(b-a)3+(a-b),2x2-![]() y2中,在有理数范围内能运用平方差公式分解的有
y2中,在有理数范围内能运用平方差公式分解的有
[ ]
给出下列多项式:
① ;②
;②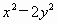 ;③-
;③- ;④
;④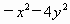 ;⑤
;⑤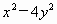 ;
;
其中在有理数范围内可以运用平方差公式分解因式的是
[ ]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com