
题目列表(包括答案和解析)
要判定一个四边形是矩形,可以先判定这个四边形是
________,再判定________(只需填写一种方法).你知道以下过程分别使用了哪种判定方法而得到矩形的吗?
(1)小红想买一条矩形的丝巾,她把原丝巾对折两次(共四层),如果原丝巾的四个角完全重合,即表明它是矩形;
(2)一台电视机的两组相对的边框已经互相平行,用直尺再测量一下电视机的两条对角线的长度就可以知道电视机屏幕边缘是否成直角;
(3)工人师傅做铝合金窗框,先做成平行四边形形状,然后将直角尺靠紧窗框的一个角,调整窗框的边缘,当直尺的两条直角边与窗框无缝隙时,说明窗框是合格的.
如图1,在直角梯形ABCD中,AD∥BC,∠B=∠A=90°,AD=a,BC=b,AB=c,
操作示例
我们可以取直角梯形ABCD的一腰CD的中点P,过点P作PE∥AB,裁掉△PEC,并将△PEC拼接到△PFD的位置,构成新的图形(如图2).
思考发现
小明在操作后发现,该剪拼方法就是先将△PEC绕点P逆时针旋转180°到△PFD的位置,易知PE与PF在同一条直线上.又因为在梯形ABCD中,AD∥BC,∠C+∠ADP=180°,则∠FDP+∠ADP=180°,所以AD和DF在同一条直线上,那么构成的新图形是一个四边形,进而根据平行四边形的判定方法,可以判断出四边形ABEF是一个平行四边形,而且还是一个特殊的平行四边形——矩形.
1.图2中,矩形ABEF的面积是 ;(用含a,b,c的式子表示)
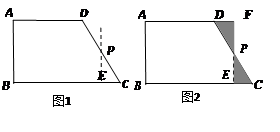
2.类比图2的剪拼方法,请你就图3(其中AD∥BC)和图4(其中AB∥DC)的两种情形分别画出剪拼成一个平行四边形的示意图.

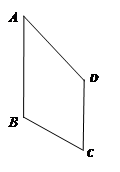
3.小明通过探究后发现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
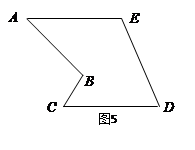
如图5的多边形中,AE=CD,AE∥CD,能否象上面剪切方法一样沿一条直线进行剪切,拼成一个平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.
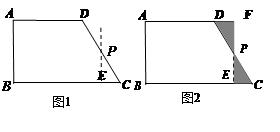
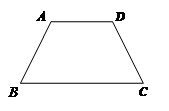
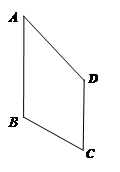

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com