练习册

  • 练习册
  • 试题
    2命题与证明 第1题. 已知四个命题:(1)如果一个数的相反数等于它本身.则这个数是0,(2)一个数的倒数等于它本身.则这个数是1,(3)一个数的算术平方根等于它本身.则这个数是1或0, (4)如果一个数的绝对值等于它本身.则这个数是正数．其中真命题有( ) A．1个 B．2个 C．3个 D．4个 答案:B 第2题. 判断下列命题的真假． ①大于锐角的角是钝角, ②如果一个实数有算术平方根.那么它的算术平方根是整数, ③如果.那么点是线段的中点． 答案:①②③假命题． 第3题. 下列命题称为公理的是 A．垂线段最短 B．同角的补角相等 C．邻角的平分线互相垂直 D．内错角相等两直线平行 答案:A 第4题. 过直线外一点有且只有一条直线与已知直线平行是 A．公理 B．定理 C．定义 D．假命题 答案:A 第5题. 下列说法中错误的是( ) A．所有的定义都是命题 B．所有的定理都是命题 C．所有的公理都是命题 D．所有的命题都是定理 答案:D 第6题. 根据命题画出图形.写出已知.求证两直线平行.同旁内角互补． 答案:已知.如图.直线.直线交.于.. 求证:． 第7题. 下列语句中不是命题的是( ) A．自然数也是整数 B．两个锐角的和为一直角 C．以为圆心为半径画圆 D．互补的角为邻补角 答案:C 第8题. 下列命题中真命题是( ) ①过一点能且只能作一条直线与已知直线垂直 ②若..则 ③一个角的余角比这个角的补角小 ④不相交的两条直线叫平行线 A．①和② B．①和③ C①②③ D①②③④ 答案:B 第9题. 举反例说明“一个角的余角大于这个角 是假命题.错误的是( ) A．设这个角是.它的余角是. B．设这个角是.它的余角是. C．设这个角是.它的余角是. D．设这个角是.它的余角是. 答案:C 第10题. 下列语句中.不是命题的句子是 A．过一点作已知直线的垂线 B．两点确定一条直线 C．钝角大于 D．凡平角都相等 答案:A 第11题. 命题“有两条边和一个角对应相等的两个三角形全等 的题设是 .结论是 .它是 命题． 答案:如果两个三角形中有两条边和一个角对应相等,这两个三角形全等,假． 第12题. 把命题不相等的角不是对顶角改为“如果那么 的形式为 ． 答案:如果两个角不相等.那么这两个角不是对顶角． 第13题. 如图..． 求证:． 答案:因为.． 所以． 即． 又.所以． 第14题. 已知:如图.....求证:． 答案:因为.. 所以.所以. 因为.所以. 所以.因为.所以． 第15题. 如图..且.那么图中与相等的角(不包括)的个数是 A．2 B．4 C．5 D．6 答案:C 第16题. 如图.在中..在上取一点.使.是的中点.是的中点.延长交的延长线于.求证:． 答案:连结.取中点.连结..为中点.为中点. 为中点..．.. .．...． 【查看更多】

     

    题目列表(包括答案和解析)

    （1）如图1，在平面直角坐标系中，△ABC的顶点坐标分别为（4，0）（8，2），（6，4）．已知△A1B1C1的两个顶点的坐标为（1，3），（2，5）．若△ABC与△A1B1C1位似，则△A1B1C1的第三个顶点的坐标为
    （3，4）或（0，4）
    （3，4）或（0，4）
    ．
    （2）在数学课上，林老师在黑板上画出如图2所示的图形（其中点B、F、C、E在同一直线上），并写出四个条件：①AB=DE，②BF=EC，③∠B=∠E，④∠1=∠2．请你从这四个条件中选出三个作为题设，另一个作为结论，组成一个真命题，并给予证明．题设：
    ①②③
    ①②③
    ；结论：
    ④
    ④
    ．（均填写序号）
    证明：

    查看答案和解析>>

    如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．
    （1）完成下面的证明：
    ∵MG平分∠BMN
    已知
    已知

    ∴∠GMN=
    1
    2
    ∠BMN
    角平分线的定义
    角平分线的定义

    同理∠GNM=
    1
    2
    ∠DNM．
    ∵AB∥CD
    已知
    已知
    ，
    ∴∠BMN+∠DNM=
    180°
    180°

    ∴∠GMN+∠GNM=
    90°
    90°

    ∵∠GMN+∠GNM+∠G=
    180°
    180°

    ∴∠G=
    90°
    90°

    ∴MG与NG的位置关系是
    MG⊥NG
    MG⊥NG

    （2）把上面的题设和结论，用文字语言概括为一个命题：
    两平行直线被第三条直线所截，同旁内角的角平分线互相垂直
    两平行直线被第三条直线所截，同旁内角的角平分线互相垂直
    ．

    查看答案和解析>>

    （1）如图1，在平面直角坐标系中，△ABC的顶点坐标分别为（4，0）（8，2），（6，4）．已知△A1B1C1的两个顶点的坐标为（1，3），（2，5）．若△ABC与△A1B1C1位似，则△A1B1C1的第三个顶点的坐标为______．
    （2）在数学课上，林老师在黑板上画出如图2所示的图形（其中点B、F、C、E在同一直线上），并写出四个条件：①AB=DE，②BF=EC，③∠B=∠E，④∠1=∠2．请你从这四个条件中选出三个作为题设，另一个作为结论，组成一个真命题，并给予证明．题设：______；结论：______．（均填写序号）
    证明：

    查看答案和解析>>

    阅读题．

    (1)如图所示，设正方形ABCD的面积为S，它的两条对角线与一组对边所围成的两个三角形面积为S1，S2，则三者之间存在的等量关系为________；

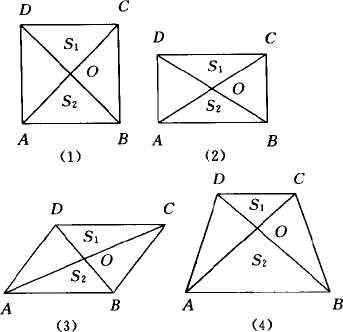
    (2)将第(1)问中的正方形改为矩形后，其余条件不变，则第(1)问中的等量关系是否成立？

    (3)将第(1)问中的正方形改为平行四边形后，依照第(1)问写一个命题并判断真假；(不要求证明)

    (4)设梯形的面积为S，梯形的两条对角线与两底边所夹的三角形面积为S1，S2，则三者之间有何等量关系，并证明你的结论；

    (5)根据(1)至(4)你可以归纳出的结论：________．

    查看答案和解析>>


    同步练习册答案