
题目列表(包括答案和解析)
| 1 | 8 |
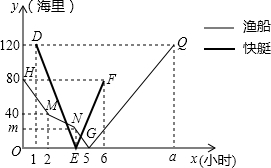 B岛位于自然环境优美的西沙群岛,盛产多种鱼类.A港、B岛、C港依次在同一条直线上,一渔船从A港出发经由B岛向C港航行,航行2小时时发现鱼群,于是渔船匀速缓慢向B港方向前行打渔.在渔船出发一小时后,一艘快艇由C港出发,经由B岛前往A港运送物资.当快艇到达B岛时渔船恰好打渔结束,渔船又以原速经由B岛到达C港.下面是两船距B港的距离y(海里)与渔船航行时间x(小时)的函数图象,结合图象回答下列问题:
B岛位于自然环境优美的西沙群岛,盛产多种鱼类.A港、B岛、C港依次在同一条直线上,一渔船从A港出发经由B岛向C港航行,航行2小时时发现鱼群,于是渔船匀速缓慢向B港方向前行打渔.在渔船出发一小时后,一艘快艇由C港出发,经由B岛前往A港运送物资.当快艇到达B岛时渔船恰好打渔结束,渔船又以原速经由B岛到达C港.下面是两船距B港的距离y(海里)与渔船航行时间x(小时)的函数图象,结合图象回答下列问题: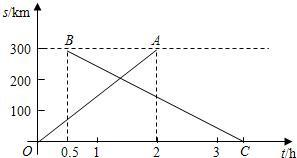
| 2 | 3 |
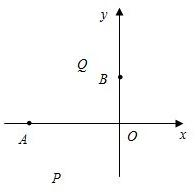 象经过点A(t1,0),B(0,t2).
象经过点A(t1,0),B(0,t2).| 7 | 2 |
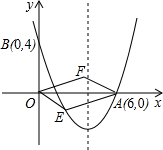 行四边形?若能,求出点E、F的坐标;若不能,请说明理由.(第(4)问不写解答过程,只写结论)
行四边形?若能,求出点E、F的坐标;若不能,请说明理由.(第(4)问不写解答过程,只写结论)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com