（2012•新区二模）在图形的全等变换中，有旋转变换，翻折（轴对称）变换和平移变换．一次数学活动课上，老师组织大家利用矩形进行图形变换的探究活动．
（1）第一小组的同学发现，在如图1-1的矩形ABCD中，AC、BD相交于点O，Rt△ADC可以由Rt△ABC经过一种变换得到，请你写出这种变换的过程．

（2）第二小组同学将矩形纸片ABCD按如下顺序进行操作：对折、展平，得折痕EF（如图2-1）；再沿GC折叠，使点B落在EF上的点B′处（如图2-2），这样能得到∠B′GC的大小，你知道∠B′GC的大小是多少吗？请写出求解过程．
（3）第三小组的同学，在一个矩形纸片上按照图3-1的方式剪下△ABC，其中BA=BC，将△ABC沿着直线AC的方向依次进行平移变换，每次均移动AC的长度，得到了△CDE、△EFG和△GHI，如图3-2．已知AH=AI，AC长为a，现以AD、AF和AH为三边构成一个新三角形，已知这个新三角形面积小于15

15

，请你帮助该小组求出a可能的最大整数值．

（4）探究活动结束后，老师给大家留下了一道探究题：
如图4-1，已知AA′=BB′=CC′=2，∠AOB′=∠BOC′=∠COA′=60°，请利用图形变换探究S_△AOB′+S_△BOC′+S_△COA′与

3

的大小关系．

以下两题请选择一题解答，若两题都答，只把第1题的分数记入学分．
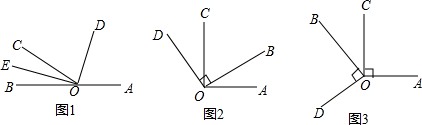
①如图1，已知射线OC在平角∠AOB的内部，且∠AOC＞∠BOC，OD平分∠AOC，OE平分∠BOC．
（1）比较∠COD与∠COE的大小，并说明理由．
（2）你能求出∠DOE的大小吗？如果能，请求出它的度数，若不能，说明理由．
（3）若∠AOB=a，你能用a表示∠DOE的度数吗？请说明理由．
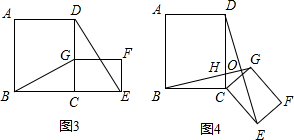
②如图2，∠AOC与∠BOD都是直角，∠BOC=50°．
（1）求∠AOB和∠DOC的度数，∠AOB和∠DOC有何大小关系？
（2）若∠BOC的具体度数不稳定，其他条件不变，这种关系仍然成立吗？说明理由．
（3）试猜想∠AOD与∠COB在数量上是相等、互余，还是互补关系？你能用推理的方法说明你的猜想是否合理吗？
（4）当∠BOD绕点O旋转到图3位置时，你原来的猜想还成立吗？说明理由．

如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：
（1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；
②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2、如图3情形．请你判断①中得到的结论是否仍然成立，并选取图2证明你的判断．
（2）将原题中正方形改为矩形（如图6），且AB=a，BC=b，CE=ka，CG=kb （a≠b，k＞0），第（1）题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．