
题目列表(包括答案和解析)
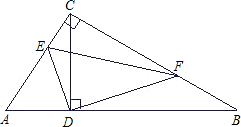 一点,且CE=
一点,且CE=| 1 |
| 3 |
| 1 |
| 3 |
| AC |
| BC |
| CD |
| BD |
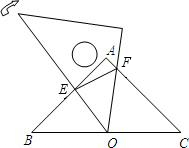
 在Rt△ABC中,∠A=90°,tanB=
在Rt△ABC中,∠A=90°,tanB=| 3 | 4 |
 | DE |
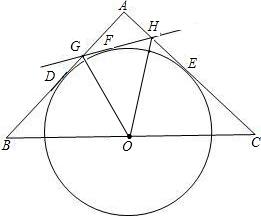 的函数关系,写出你的探究过程并确定自变量x的取值范围,并说明当x=y时F点的位置.
的函数关系,写出你的探究过程并确定自变量x的取值范围,并说明当x=y时F点的位置.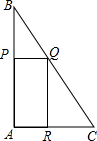 在Rt△ABC中,∠A=90°,tanB=
在Rt△ABC中,∠A=90°,tanB= ,点P在线段AB上运动,点Q、R分别在线段BC,AC上,且使得四边形APQR是矩形.设AP的长是x,矩形APQR面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线上的一部分.
,点P在线段AB上运动,点Q、R分别在线段BC,AC上,且使得四边形APQR是矩形.设AP的长是x,矩形APQR面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线上的一部分.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com