
题目列表(包括答案和解析)
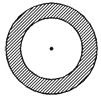 小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.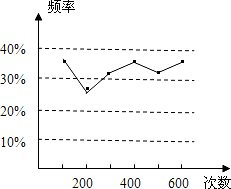 如图所示,则符合这一结果的实验可能是( )
如图所示,则符合这一结果的实验可能是( )| A、掷一枚正六面体的骰子,出现5点的概率 | B、掷一枚硬币,出现正面朝上的概率 | C、任意写出一个整数,能被2整除的概率 | D、一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率 |
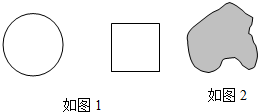 一定距离外向圆和正方形内掷小石子,谁投进的次数多谁就胜.
一定距离外向圆和正方形内掷小石子,谁投进的次数多谁就胜.通过实验的方法用频率估计概率的大小,必须要求实验是在 的条件下进行.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com