
题目列表(包括答案和解析)
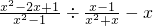 ,其中x=2007”甲同学把“x=2007”错抄成“x=2070”,但他计算的结果也是正确的,你说这是怎么一回事?
,其中x=2007”甲同学把“x=2007”错抄成“x=2070”,但他计算的结果也是正确的,你说这是怎么一回事?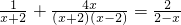

| • |
| 2 |
| • |
| 2 |
| • |
| 2 |
| 2 |
| 9 |
| • |
| 2 |
| 2 |
| 9 |
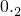 .
.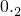 ①.等式两边同时乘以10,得10x=
①.等式两边同时乘以10,得10x=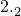 ②.
②.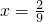 .∴
.∴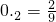
 .
. ①.等式两边同时乘以10,得10x=
①.等式两边同时乘以10,得10x= ②.
②. .
. 请参照以上解法求出国王输给阿基米德的米粒数(用幂的形式表示)
请参照以上解法求出国王输给阿基米德的米粒数(用幂的形式表示)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com