
题目列表(包括答案和解析)
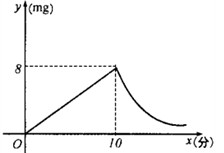
为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量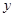 (mg)与燃烧时间
(mg)与燃烧时间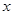 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后,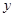 与
与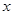 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求室内每立方米空气中的含药量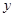 与
与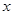 的函数关系式;
的函数关系式;
(2)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?
(3)经医学论证,只有当每立方米空气中的含药量不低于4mg且持续的时间不少于12分钟时,才认为消毒有效,请问本次消毒有效么?请说明理由。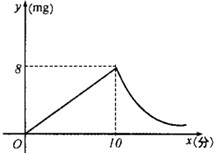
为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量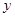 (mg)与燃烧时间
(mg)与燃烧时间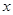 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后,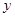 与
与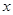 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求室内每立方米空气中的含药量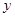 与
与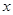 的函数关系式;
的函数关系式;
(2)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?
(3)经医学论证,只有当每立方米空气中的含药量不低于4mg且持续的时间不少于12分钟时,才认为消毒有效,请问本次消毒有效么?请说明理由。
 (mg)与燃烧时间
(mg)与燃烧时间 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后, 与
与 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题: 与
与 的函数关系式;
的函数关系式;

 2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表:
2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表:| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 12 | 6 | 4 | 3 |
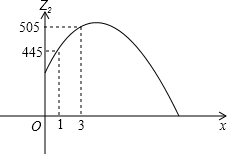
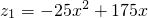 ;进入4月份,该超市每周的蘑菇销售价格稳定在3元/千克,每周的销售量z2(千克)与周数x(1≤x≤4,且x为整数)所满足的函数关系式为
;进入4月份,该超市每周的蘑菇销售价格稳定在3元/千克,每周的销售量z2(千克)与周数x(1≤x≤4,且x为整数)所满足的函数关系式为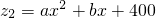 ,且函数图象为下图所示:
,且函数图象为下图所示: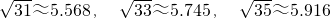 )
)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com