
题目列表(包括答案和解析)
 如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.
分析 (1)利用60°角![]() 的正弦值列式计算即可得解;
的正弦值列式计算即可得解;
(2)①连接CF并延长交BA的延长线于点G,利用“角边角”证明△AFG和△CFD全等,根据全等三角形对应边相等可得CF=GF,AG=CD,再利用直角三角形斜边上的中线等于斜边的一半可得EF=GF,再根据A![]() B、BC的长度可得AG=AF,然后利用等边对等角的性质可得∠AEF=∠G=∠AFG,
B、BC的长度可得AG=AF,然后利用等边对等角的性质可得∠AEF=∠G=∠AFG,![]() 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G,然后推出∠EFD=3∠AEF,从而得解;
根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G,然后推出∠EFD=3∠AEF,从而得解;
②设BE=x,在Rt△BCE中,利用勾股定理表示出CE2,表示出EG的长度,在Rt△CEG中,利用勾股定理表示出CG2,从而得到CF2,然后相减并整理,再根据二次函数的最值问题解答.
如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
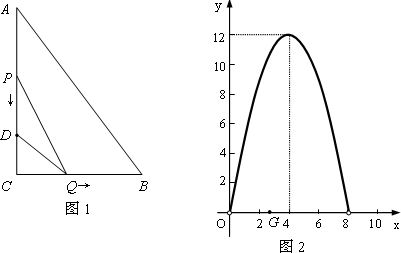
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点(0<OG<6,过G作EF垂直于x轴,分别交y1、y2于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
解:
如图,在一个等边三角形EFG的内部做一个矩形ABCD,其中等边三角形的边长为40 cm,点C和点D分别在边EF、EG上.

(1)如果设矩形的一边AB=x cm,那么AD的长度如何表示?
(2)设矩形的面积为y cm,当x取何值时,y的值最大,最大值是多少?
(提示:过点E作EM⊥GF,交CD于点N)
(1)EM的长为________cm.
(2)由DC∥GF,得△________∽△________.
所以DC∶GF=EN∶EM.
(3)设矩形的一边AB=x cm,则x∶40=(EM-AD)∶EM,解得AD=________.
(4)y与x之间的表达式是________.
(5)因为a________0,所以y有最________值.当x=________时,矩形的面积有最大值,最大值是________.
析一析:(1)先求出EM的长;
(2)由DC∥GF可以得出两个三角形相似;
(3)利用相似三角形的性质,求出AD的长;
(4)由矩形的面积=AD·AB,可以求出y与x之间的关系式;
(5)利用y与x之间的关系式可以解答第(2)问吗?试完成下面的解答过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com