
题目列表(包括答案和解析)
(本题满分12分) 如图1,在底面积为l00cm2、高为20cm的长方体水槽内放人一个圆柱形烧杯.以恒定不变的流量速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变.水槽中水面上升的高度h与注水时间t之间的函数关系如图2所示.
(1)写出函数图象中点A、点B的实际意义;
(2)求烧杯的底面积;
 (3)若烧杯的高为9cm,求注水的速度及注满水槽所用的时间.
(3)若烧杯的高为9cm,求注水的速度及注满水槽所用的时间.
 .
. 的图象性质.
的图象性质.| x | … |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | | | | | | | | … |
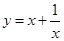 (x>0)的最小值.
(x>0)的最小值.
(本题满分12分)
问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为![]() .
.
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数![]() 的图象性质.
的图象性质.
① 填写下表,画出函数的图象:
| x | … |
|
|
| 1 | 2 | 3 | 4 | … |
| y | … |
|
|
|
|
|
|
| … |
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数![]() (x>0)的最小值.
(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.

(本题满分12分)
问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为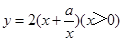 .
.
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数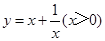 的图象性质.
的图象性质.
① 填写下表,画出函数的图象:
|
x |
… |
|
|
|
1 |
2 |
3 |
4 |
… |
|
y |
… |
|
|
|
|
|
|
|
… |
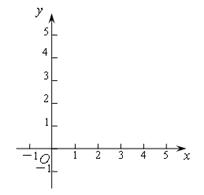
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数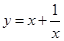 (x>0)的最小值.
(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
(本题满分12分,每小题6分)
(1) 在如图所示的平面直角坐标系中,先画出△OAB 关于y轴对称的图形,再画出△OAB绕点O旋转180°后得到的图形.
(2)先阅读后作答:我们已经知道,根据几何图形的面积 关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:(2a +b)( a +b) = 2a2 +3ab +b2,就可以用图22-1的面积关系来说明.



① 根据图22-2写出一个等式 ;
② 已知等式:(x +p)(x +q)=x2 + (p +q) x + pq,请你画出一个相应的几何图形加以说明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com