
题目列表(包括答案和解析)
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 东方 | 10 | 4 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 蓝天 | 14 | 9 | 5 | 23 |
| 雄鹰 | 14 | 7 | 7 | 21 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
| 钢铁 | 14 | 0 | 14 | 14 |
列一元二次方程解下列应用题(每小题6分,共18分)
(1)已知两个正方形的面积之和为89,周长之差为12, 求这两个正方形的边长。
(2)有一人患了流感,经两轮传染后共有144人患了这种疾病,每轮传染中平均一个人传染了几人?
(3)据有关部门统计,我省农作物秸秆资源巨大,但合理利用量十分有限,2009年利用率只有30℅,大部分秸秆被直接焚烧,假定我省产生的农作物秸秆总量不变,且合理利用量的增长率相同,要使2011年的利用率提高到60℅,求每年的增长率。(可能用到的数据:![]() )
)
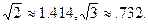 )
)列一元二次方程解下列应用题(每小题6分,共18分)
(1)已知两个正方形的面积之和为89,周长之差为12, 求这两个正方形的边长。
(2)有一人患了流感,经两轮传染后共有144人患了这种疾病,每轮传染中平均一个人传染了几人?
(3)据有关部门统计,我省农作物秸秆资源巨大,但合理利用量十分有限,2009年利用率只有30℅,大部分秸秆被直接焚烧,假定我省产生的农作物秸秆总量不变,且合理利用量的增长率相同,要使2011年的利用率提高到60℅,求每年的增长率。(可能用到的数据: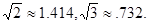 )
)
列一元二次方程解下列应用题(每小题6分,共18分)
(1)已知两个正方形的面积之和为89,周长之差为12, 求这两个正方形的边长。
(2)有一人患了流感,经两轮传染后共有144人患了这种疾病,每轮传染中平均一个人传染了几人?
(3)据有关部门统计,我省农作物秸秆资源巨大,但合理利用量十分有限,2009年利用率只有30℅,大部分秸秆被直接焚烧,假定我省产生的农作物秸秆总量不变,且合理利用量的增长率相同,要使2011年的利用率提高到60℅,求每年的增长率。(可能用到的数据: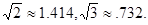 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com