数学课上，张老师给出了问题：
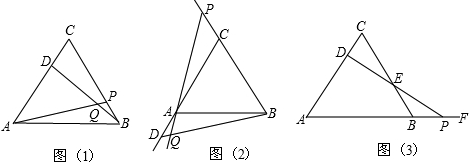
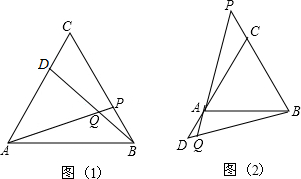
如图（1），△ABC为等边三角形，动点D在边CA上，动点P边BC上，若这两点分别从C、B点同时出发，以相同的速度由C向A和由B向C运动，连接AP，BD交于点Q，两点运动过程中AP=BD成立吗？请证明你的结论；
经过思考，小明展示了一种正确的解题思路：由△ABP≌△BCD，从而得出AP=BD．
在此基础上，同学们作了进一步探究：
（1）小颖提出：如果把原题中“动点D在边CA上，动点P边BC上，”改为“动点D，P在射线CA和射线BC上运动”，其他条件不变，如图（2）所示，两点运动过程中∠BQP的大小保持不变．请你利用图（2）的情形，求证：∠BQP=60°；
（2）小华提出：如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动，连接PD交BC于E”，其他条件不变，如图（3），则动点D，P在运动过程中，DE始终等于PE．你认为小华的观点正确吗？如果正确，写出证明过程．